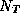 we expect to arrive on
the plate with positions in the interval
we expect to arrive on
the plate with positions in the interval 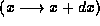 is
is
The picture we have of an experiment involves two phases, (1) a
probability wave propagates through the apparatus, (2) particles
arrive according to the distribution given by the square of the
amplitude of the wave. If we repeat our experiment many times in a
unit time interval, as in a two-slit Young interference experiment
where the source sends many particles per second through the apparatus,
then the probability distribution (as in Figure 3) gives us the
average rate of arrival of photons in each region of the plate. If
we wait a sampling time T and the source emits photons at a rate of
I, then the average number of particles 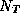 we expect to arrive on
the plate with positions in the interval
we expect to arrive on
the plate with positions in the interval 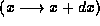 is
is
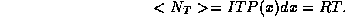
This is just the sampling time T times some average rate R
determined by the distribution  . Because of the randomness
inherent in the process, however, if we were to repeat the experiment of
counting photons arriving in the interval
. Because of the randomness
inherent in the process, however, if we were to repeat the experiment of
counting photons arriving in the interval  during intervals of time T many times, we would not find the same
number of photons
during intervals of time T many times, we would not find the same
number of photons  in each experiment. There will be a distribution in
the values of
in each experiment. There will be a distribution in
the values of  as in Figure 11 below.
as in Figure 11 below.  is a new random
variable, with an average value
is a new random
variable, with an average value  and a variance of its own.
Using very general arguments we will now demonstrate the result quoted in
class
and a variance of its own.
Using very general arguments we will now demonstrate the result quoted in
class
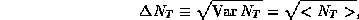
Our arguments are very general and will apply to nearly all counting experiments. The distribution we are discussion is so important that it bears its own name, the Poisson distribution.

We begin by showing that  , from which
, from which
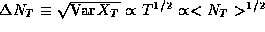 will follow quickly. To show
will follow quickly. To show 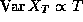 we note use the facts that the variance of independent random
variables add and that the photons in the experiment arrive randomly or
independently of one another.
we note use the facts that the variance of independent random
variables add and that the photons in the experiment arrive randomly or
independently of one another.
This means that if we were, for
instance, to divide our counting time interval from 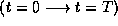 into two separate intervals, interval 1 from
into two separate intervals, interval 1 from 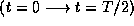 and interval 2 from
and interval 2 from 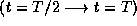 , then we could define two independently
distributed random variables
, then we could define two independently
distributed random variables  and
and 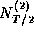 ,
which each represent a counting experiment of length
,
which each represent a counting experiment of length  but carried
out at two different times.
The sum of these two random variables is just the total number of
particles arriving in our original time interval, so that
but carried
out at two different times.
The sum of these two random variables is just the total number of
particles arriving in our original time interval, so that
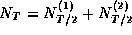 . Finally, we know that as long as
the source intensity is constant, the counting statistics do not
depend on when we do our counting; they depend only on how
long we do the counting. Thus, we may take
. Finally, we know that as long as
the source intensity is constant, the counting statistics do not
depend on when we do our counting; they depend only on how
long we do the counting. Thus, we may take
 ,
where
,
where 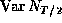 is the variance of any counting experiment
over a length of time
is the variance of any counting experiment
over a length of time 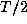 at any point in time. We have then,
at any point in time. We have then,

We could have, instead of just two divisions, divided our time interval T into many
small time intervals of length  . Our total time T is then
divided into
. Our total time T is then
divided into  intervals and we find,
intervals and we find,
We thus have shown that 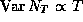 by just using the fact that
the variances of independent random variables add and by
dividing the counting interval into a set of small time intervals whose
number varies in proportion to the sampling time interval.
by just using the fact that
the variances of independent random variables add and by
dividing the counting interval into a set of small time intervals whose
number varies in proportion to the sampling time interval.
We now need only evaluate the proportionality constant 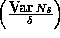 . This is most easily
done as
the time interval
. This is most easily
done as
the time interval 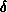 becomes very small. As
becomes very small. As  , the probability of
counting zero photons
, the probability of
counting zero photons 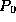 approaches unity,
approaches unity,  ; the
probability of counting a single photon
; the
probability of counting a single photon  is very small
is very small 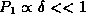 ; and the probability of counting two or more
photons is negligible,
; and the probability of counting two or more
photons is negligible,  . We can now
determine
. We can now
determine  from the average rate. Counting over a time
from the average rate. Counting over a time 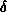 ,
on average we expect
,
on average we expect 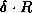 photons and so,
photons and so,

The variance is then
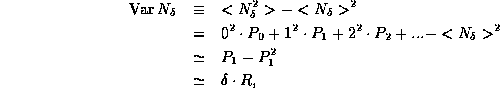
where we ignore terms 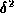 and higher. We now have our
proportionality constant,
and higher. We now have our
proportionality constant,

Combining this with (3), we have our final result,

and so

Note that this result is very general and not restricted to photons. Our derivation depends only on the counting of independent random events and so could apply equally well to counting either the arrival of electrons, the decay of nuclei or the arrival of cars in the parking lot at the shopping mall. On Problem Set 2, you showed how to apply this result to estimate the value of Planck's constant from observations you can make in your own room at night.