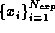If we now want to compute the average value of x, we can proceed
either in the traditionally way of imagining a whole series of
measurements of x,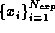 
and computing the
average as
or, we may get the same result by using the random variable X,
The key difference between (1) and (2) is the conceptual focus. In (1) the sum is over the different measurements made; this forces us to think of each individual measurement. But in (2), the sum is over the values of the possible outcomes of the experiment and uses the probability distribution explicitly; this frees us to think in terms of the experiment as a whole, as a series of potential outcomes occurring with different probabilities. The form (2) is much closer to nature and more convenient for our purposes. We will use it throughout this course. In this note, we will give proofs both in the more familiar form (1) and the newer form (2) to help orient you to it.
The central theorem regarding the averages of random variables is that the average of a sum of random variables is the sum of their averages. This is always true regardless of any correlation (which we will describe in detail in section (5)) which may exist between the variables. In the individual measurement picture, this is easy to see.
