


Next: Complex representation to the
Up: ps2
Previous: A bouncy ride
Contents
- (a)
- Show, by verifying in the equation of motion and counting the free parameters, that the general solution to the equation of motion of a simple
harmonic oscillator (SHO) can be written also as:
![\begin{displaymath}
x(t) = x_{\rm eq} + \frac{1}{2}\left[\underline{A}e^{i\omega_o t} +
\underline{A}^* e^{-i\omega_o t}\right]\;,
\end{displaymath}](img28.png) |
(1) |
where 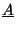 is the complex amplitude and
is the complex amplitude and
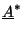 , its complex conjugate.
, its complex conjugate.
- (b)
- Express
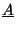 and
and
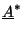 in terms
of
in terms
of 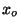 ,
, 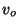 ,
, 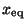 , and
, and 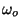 .
.
Tomas Arias
2003-09-03