


Next: Other types of damping
Up: ps3
Previous: Application: care crossing bridges
Contents
- (a)
- From the general solution
determine the total (potential plus kinetic) energy of an undamped oscillator in terms of
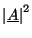 ,
, 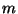 and
and
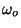 .
.
Hint: Use the fact that
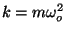 .
.
- (b)
- From the general solution
compute the average kinetic energy and the average potential energy of the undamped oscillator in terms of
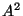 , and show that they are equal.
, and show that they are equal.
Hint: The average
values of both 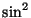 and
and 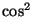 are
are 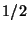 .
.
- (c)
- Using the fact that the work done per unit time (power)
against any force is
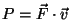 , show that
for the drag force described in lecture, the total energy
, show that
for the drag force described in lecture, the total energy 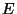 (kinetic plus potential) of a damped oscillator obeys
(kinetic plus potential) of a damped oscillator obeys
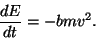 |
(2) |
How does the average of this energy loss 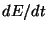 compare to
the average kinetic energy?
compare to
the average kinetic energy?
- (d)
- If the damping
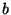 is relatively small, the result in (b) that the average kinetic energy is the same as the average
potential energy is a very good approximation. Under this
approximation, use your result in (c) to show that on average
is relatively small, the result in (b) that the average kinetic energy is the same as the average
potential energy is a very good approximation. Under this
approximation, use your result in (c) to show that on average
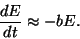 |
(3) |
- (e)
- The solution to the equation in (d) is that the
energy decays exponentially as
Explain (in a brief sentence or two) why the exponent here
is ``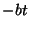 '' whereas the exponent in the general solution for damped
harmonic motion is ``
'' whereas the exponent in the general solution for damped
harmonic motion is ``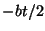 ''.
''.



Next: Other types of damping
Up: ps3
Previous: Application: care crossing bridges
Contents
Tomas Arias
2003-09-08