


Next: Energy in oscillators
Up: ps3
Previous: Closer look at the
Contents
To avoid the possibility of driving bridges into large oscillations by
the periodic impact of footsteps, the US Army infantry now never
marches instep across bridges. In this problem, we will evaluate
whether this concern is realistic by computing how closely timed the
footsteps must be to match a bridge's natural frequency. To answer
this question, we shall use a simple model of the bridge as a driven,
damped oscillator.
Within this model, we take the march steps to correspond to a periodic
driving force
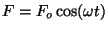 , where
, where
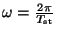 with
with
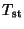 being the
time between the footsteps of a unit marching in formation. To make
the model realistic, we assume the following information:
being the
time between the footsteps of a unit marching in formation. To make
the model realistic, we assume the following information:
- (a)
- Use the above information to extract the
numerical parameters (
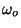 ,
, 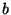 ) needed to make a computer or
calculator plot of
) needed to make a computer or
calculator plot of
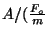 ) versus the marching frequency
) versus the marching frequency
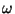 , where
, where 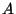 is the amplitude of the bridge's oscillation.
Turn in a properly labeled sketch or a copy of the resulting
plot.
is the amplitude of the bridge's oscillation.
Turn in a properly labeled sketch or a copy of the resulting
plot.
- (b)
- Read off from your plot the range within which
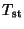 must fall in order for the amplitude to be within 1/2 of its
maximum value. (An approximate range read off from your plot
is fine.)
must fall in order for the amplitude to be within 1/2 of its
maximum value. (An approximate range read off from your plot
is fine.)
- (c)
- Comment in a brief sentence or two on whether you
feel the concern about driving such a bridge into resonance is
realistic.



Next: Energy in oscillators
Up: ps3
Previous: Closer look at the
Contents
Tomas Arias
2003-09-08
![]() , where
, where
![]() with
with
![]() being the
time between the footsteps of a unit marching in formation. To make
the model realistic, we assume the following information:
being the
time between the footsteps of a unit marching in formation. To make
the model realistic, we assume the following information: