


Next: Application: care crossing bridges
Up: ps3
Previous: Contents
Contents
In lecture we derived an expression for the complex amplitude
 of a driven and damped harmonic oscillator, with
real amplitude
of a driven and damped harmonic oscillator, with
real amplitude 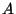 and initial phase
and initial phase
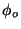 ,
,
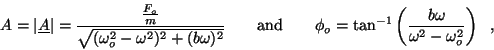 |
(1) |
where
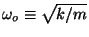 is the natural frequency of
the system.
is the natural frequency of
the system.
In order to better appreciate the physical significance of these
quantities and their frequency dependence, it is useful to
plot them versus frequency and to identify certain important
parameters of these plots. In this problem you will do this, starting
from analyzing
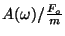 and
and
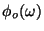 in various
limits1:
in various
limits1:
- (a)
- Evaluate
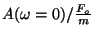 and
and
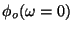 .
.
- (b)
- Evaluate
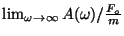 and
and
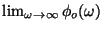 .
.
- (c)
- Show that
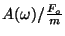 has a maximum at
has a maximum at
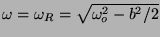 if
if
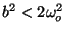 . Express the value of
. Express the value of
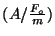 at the maximum in
terms of
at the maximum in
terms of 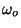 and
and 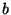 .
.
Hint: Argue that the ratio of two
positive expressions has a maximum when the denominator has a
minimum. Then show that the denominator of 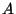 in eq. (1) has a minimum at
in eq. (1) has a minimum at
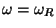 by checking
that
by checking
that
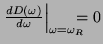 for
the function
for
the function
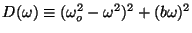 .
.
- (d)
- In the limit
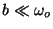 , show that
, show that
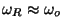 and that
and that
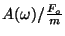 is approximately
equal to
is approximately
equal to
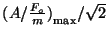 at each of the frequencies
at each of the frequencies
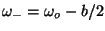 and
and
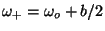 . Compute the `frequency
band-width'
. Compute the `frequency
band-width'
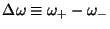 .
.
- (e)
- Sketch plots of the functions
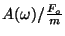 and
and
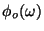 in the limit
in the limit
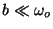 . Label the quantities
. Label the quantities 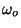 ,
,
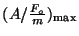 , and
, and 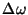 on your plot.
on your plot.
Note: For this and
other plots, you may plot the function on a plotting calculator or
computer and then just sketch the basic shape of what you see. (You
need not obtain a printout.) However, it is important that you
label key points on your sketches (such as the position, width and
height of the maxima) in terms of the basic quantities in the
problem.



Next: Application: care crossing bridges
Up: ps3
Previous: Contents
Contents
Tomas Arias
2003-09-08
![]() of a driven and damped harmonic oscillator, with
real amplitude
of a driven and damped harmonic oscillator, with
real amplitude ![]() and initial phase
and initial phase
![]() ,
,
![]() and
and
![]() in various
limits1:
in various
limits1:
![]() in eq. (1) has a minimum at
in eq. (1) has a minimum at
![]() by checking
that
by checking
that
![]() for
the function
for
the function
![]() .
.