


Next: Wave equation fundamentals
Up: ps4
Previous: Wave kinematics: particle speed
Contents
A string setup as in our physical realization for studying waves is
plucked at its center. (See Figure 1, next page.) The
mass of the string is 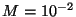 kg, its length is
kg, its length is 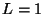 m, the
applied tension is
m, the
applied tension is 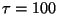 N, and the string can sustain a maximum
tension of
N, and the string can sustain a maximum
tension of
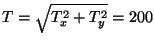 N before breaking.
N before breaking.
- (a)
- What is the maximum distance
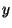 (indicated in the
figure) by which the string can be plucked before breaking?
(indicated in the
figure) by which the string can be plucked before breaking?
- (b)
- If the string is held in the plucked position with
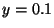 m and then released,
what will be the initial acceleration of each point of the string
with
m and then released,
what will be the initial acceleration of each point of the string
with 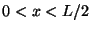 ? For each point with
? For each point with 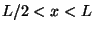 ?
?
Hint: Use
the wave equation derived in class.
Note: You
may find it fun to think about the acceleration of the chunk at
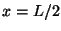 and what this all means in terms of how the string will
move once released! We will answer that question later when we have the
general solution to the wave equation.
and what this all means in terms of how the string will
move once released! We will answer that question later when we have the
general solution to the wave equation.
Tomas Arias
2003-09-17
![]() kg, its length is
kg, its length is ![]() m, the
applied tension is
m, the
applied tension is ![]() N, and the string can sustain a maximum
tension of
N, and the string can sustain a maximum
tension of
![]() N before breaking.
N before breaking.