


Next: Deriving your own wave
Up: ps4
Previous: Forces on a string
Contents
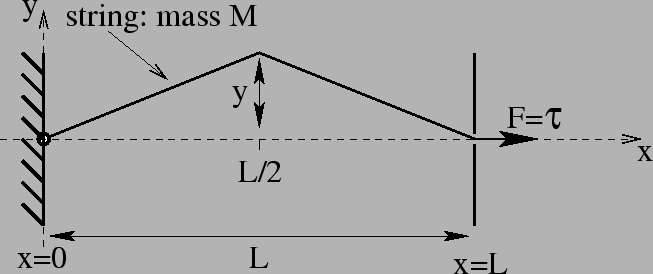
Figure 1:
String plucked at its center to a distance 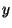 .
.
|
|
A standing wave on a string of mass 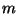 fixed at both ends (
fixed at both ends (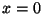 and
and 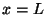 ) is described by
) is described by
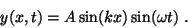 |
(1) |
Express all answers below in terms of the fundamental quantities 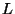 ,
,
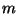 ,
, 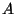 ,
, 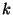 , and
, and 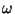 .
.
- (a)
- What is the
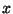 -component of the force due to the string
on the fixed point
-component of the force due to the string
on the fixed point 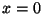 ? (Remember, the string is under tension
so it pulls on whatever is holding it.)
? (Remember, the string is under tension
so it pulls on whatever is holding it.)
- (b)
- What is the
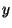 -component of the force due to the string
on the fixed point
-component of the force due to the string
on the fixed point 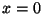 at any time
at any time 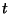 .
.
- (c)
- Consider a tiny chunk of string of length
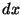 between
between 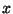 and
and 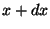 . Find the
. Find the 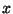 - and
- and 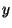 -components of the
force on the left side of this chunk (at
-components of the
force on the left side of this chunk (at 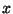 ) due to the rest of the string.
) due to the rest of the string.
- (d)
- Find the
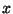 - and
- and 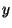 -components of the force on the
right side of this chunk (at
-components of the force on the
right side of this chunk (at 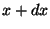 ) due to the rest of the string.
) due to the rest of the string.
- (e)
- Find the net force on the chunk.
- (f)
- Verify that
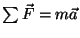 works for the
chunk in the limit
works for the
chunk in the limit
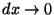 . (Note that you should be
able to do better than saying
. (Note that you should be
able to do better than saying 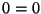 .)
.)
- (g)
- The net force
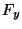 on the chunk in the
on the chunk in the 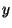 -direction is
proportional is to its displacement
-direction is
proportional is to its displacement 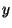 from equilibrium. Use this
to compute an effective spring constant
from equilibrium. Use this
to compute an effective spring constant 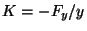 .
Compute the frequency you would expect from an object
of mass equal to the mass of the chunk tied to a spring of constant
.
Compute the frequency you would expect from an object
of mass equal to the mass of the chunk tied to a spring of constant
 , and compare to
, and compare to  .
.



Next: Deriving your own wave
Up: ps4
Previous: Forces on a string
Contents
Tomas Arias
2003-09-17
![]() fixed at both ends (
fixed at both ends (![]() and
and ![]() ) is described by
) is described by