


Next: Normal modes
Up: ps4
Previous: Wave equation fundamentals
Contents
Take the same string system from class lecture and the lecture notes,
but with drag on each chunk of the string contributing an addition
force
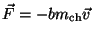 .
.
- (a)
- Redraw the force-body diagram of Figure 2 from
the lecture notes ``Intro to Waves'' including the new force.
Explain (briefly, one or two short sentences) why this
force does not affect motion in the
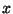 direction and hence does not
modify Eq. (7) in the notes.
direction and hence does not
modify Eq. (7) in the notes.
- (b)
- Following the analysis of Section 4.2.2 of the lecture
notes, rewrite in their new form any of Eq. (8), Eq. (11)
and Eq. (13) which change due to the presence of the new force.
Hint: You should find in the end that your new equation of motion is
equivalent to
where
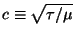 .
.
- (c)
- How quickly will the drag cause the amplitude of a standing
wave to decay to
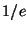 of its original amplitude?
of its original amplitude?
Hint: The answer is 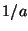 if the solution to the wave equation
has the form
if the solution to the wave equation
has the form
To find 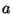 , assume a solution with the complex representation
, assume a solution with the complex representation
where
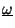 is a complex frequency, solve for
is a complex frequency, solve for
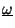 , and then take
, and then take
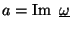 .
.



Next: Normal modes
Up: ps4
Previous: Wave equation fundamentals
Contents
Tomas Arias
2003-09-17
![]() .
.