


Next: About this document ...
Up: ps4
Previous: Normal modes
Contents
Prof. McEuen in our Department of Physics studies the vibrations of
tiny tubes (with nanometer diameter!) made entirely of carbon.
The propagation of transverse waves along such tubes is described
by the modified wave equation
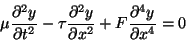 |
(2) |
where 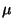 and
and 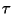 (as in lecture) are the the linear mass density
and tension respectively, and
(as in lecture) are the the linear mass density
and tension respectively, and 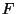 is an elastic parameter independent
of the tension and characteristic of the nanotube.
is an elastic parameter independent
of the tension and characteristic of the nanotube.
Note: This
modified equation also describes wires with stiffness (such as steel
piano wires) rather than simple strings, something about which an
astute student in the morning section asked.
- (a)
- Show that the standing wave
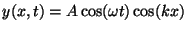 is a solution to the nanotube wave
equation (2), and derive the dispersion
relation
is a solution to the nanotube wave
equation (2), and derive the dispersion
relation 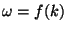 .
.
- (b)
- Typical values for these tubes are
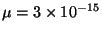 kg/m,
kg/m,
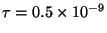 N, and
N, and
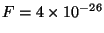 N
N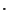 m. Prof. McEuen's tubes are typically
1
m. Prof. McEuen's tubes are typically
1  m=
m=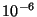 m in length. Assuming a wavelength of 2
m in length. Assuming a wavelength of 2 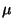 m for
the fundamental (lowest frequency) mode, how important is the
correction term
m for
the fundamental (lowest frequency) mode, how important is the
correction term 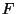 ? To answer this, compute the ratio
? To answer this, compute the ratio
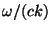 where
where 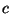 is the speed you would expect for a normal
string; i.e., if the new,
is the speed you would expect for a normal
string; i.e., if the new, 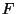 term were not there. Given your results,
for work good to a few percent, should Prof. McEuen consider the
term were not there. Given your results,
for work good to a few percent, should Prof. McEuen consider the 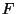 term for the first few modes of his tubes?
term for the first few modes of his tubes?
- (c)
- Below what wavelength (in Angstroms, 1 Å=
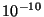 m)
does the new
m)
does the new 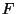 -term change the frequency significantly?
Specifically, determine the wavelength
-term change the frequency significantly?
Specifically, determine the wavelength 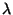 such that
the frequency is twice as high as you would expect from the usual
dispersion relation
such that
the frequency is twice as high as you would expect from the usual
dispersion relation 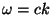 .
.



Next: About this document ...
Up: ps4
Previous: Normal modes
Contents
Tomas Arias
2003-09-17