


Next: About this document ...
Up: ps7
Previous: Function transformations
Contents
An industrious student decides to experiment with the effects of
the damped boundary condition from Problem 6 of Prelim 1,
where 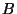 is the bulk modulus of the gas in
the tube and
is the bulk modulus of the gas in
the tube and 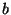 the damping coefficient in the shock absorber. (See
Figure 3.)
the damping coefficient in the shock absorber. (See
Figure 3.)
Figure 3:
Boundary condition with drag from Prelim 1
|
|
- (a)
- Following the procedure from class and in the lecture
notes, determine the form of the reflected pulse
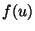 in terms of
the incoming pulse
in terms of
the incoming pulse 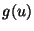 where the general solution is
where the general solution is
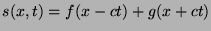 .
.
Note: Because the shock absorber is on the left of the tube, the
incoming pulse ``g'' is traveling from right to left and thus
has a ``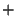 '' sign in front of the factor of
'' sign in front of the factor of 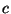 . Your task is to
solve for the reflected pulse ``f'', which travels from left to right.
. Your task is to
solve for the reflected pulse ``f'', which travels from left to right.
Hint: You should check your answer by investigating the limits
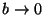 and
and
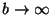 .
.
- (b)
- By experimenting with shock absorbers with
different damping coefficients
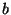 , the student
finds--amazingly--that she can send a sound pulse down the tube
without any reflection coming back! Find the value(s) of
, the student
finds--amazingly--that she can send a sound pulse down the tube
without any reflection coming back! Find the value(s) of 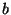 for
which no reflection occurs. Express your answer in terms of the
``impedance''
for
which no reflection occurs. Express your answer in terms of the
``impedance''
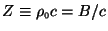 of the gas in the tube.
of the gas in the tube.
Note: Proper termination of waveguides through
impedance matching like this to avoid unwanted reflections is
very important in many electronic communications applications.



Next: About this document ...
Up: ps7
Previous: Function transformations
Contents
Tomas Arias
2003-10-15

