


Next: Sums over Histories
Up: Transmission and Reflection in
Previous: Transmission and Reflection in
Contents
The first way involves using boundary conditions at 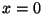 and
and 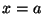 :
:
- (a)
- Using the boundary condition at
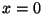 , show that the motion of
the light string is described by
, show that the motion of
the light string is described by
![$\displaystyle y_0(x<a,t)=\Re [e^{-i\omega t} \underline{D} \sin(k_0 x)].$](img30.png) |
(5) |
How is the coefficient
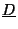 related to
related to
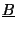 and
and
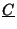 ?
?
- (b)
- Write down the equations that
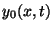 and
and 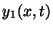 should
satisfy at
should
satisfy at 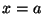 . What is the physical meaning of each equation?
. What is the physical meaning of each equation?
- (c)
- Solve these equations to obtain
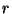 . Express your answer in
terms of
. Express your answer in
terms of 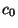 ,
, 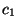 ,
, 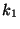 , and
, and 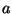 .
.
Tomas Arias
2003-10-22
![]() and
and ![]() :
: