


Next: Interference with an Off-Axis
Up: ps9
Previous: Reflection Grating
Contents
Consider once again the reflection grating in Fig. 2. It is now
illuminated with a mixture of light with two wavelengths, 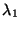 and
and
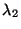 .
.
- (a)
- Find the positions of the principle maxima (in terms of
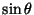 ) for each
) for each 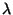 . Sketch (on the same plot)
the interference patterns for each
. Sketch (on the same plot)
the interference patterns for each 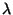 . (You can choose
any value of
. (You can choose
any value of 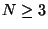 for your sketches.) Using the
sketches, explain why the grating can be used to separate, or
``resolve'', the different wavelengths.
for your sketches.) Using the
sketches, explain why the grating can be used to separate, or
``resolve'', the different wavelengths.
- (b)
- The width of a principal maximum can be defined as
the distance (in terms of
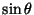 ) between the two
minima neighbouring the maximum. Find the width of the
principle maxima for each
) between the two
minima neighbouring the maximum. Find the width of the
principle maxima for each 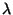 .
.
- (c)
- Consider the situation when the two wavelengths are very close
to each other,
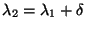 . What is the
minimal value of
. What is the
minimal value of 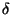 for which these waves can still be
resolved?
for which these waves can still be
resolved?
- (d)
- Sketch (on the same plot) the interference patterns for two
wavelengths that are too close to each other to be resolved.
(Again, choose any
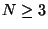 .)
.)



Next: Interference with an Off-Axis
Up: ps9
Previous: Reflection Grating
Contents
Tomas Arias
2003-11-09
![]() and
and
![]() .
.