Interference with an Off-Axis Source

Consider again the reflecting grating of problems 2, 3. The distant source has been moved so that light no longer falls on the grating normally, but at an angle 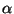$\alpha$, as shown in Fig. 3. In this problem, you will learn how this change affects the interference pattern seen by a distant observer.

(a)

Consider two waves. ``Wave 0'' has been emitted by the source, reflected by the leftmost reflecting groove (``groove 0''), and observed by a distant observer viewing the grating at angle 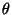$\theta$. ``Wave 1'' has been emitted by the same source, reflected by the second groove on the left (``groove 1''), and then observed by the same observer. What is the difference in the paths travelled by waves 0 and 1? What is their phase difference when they reach the observer?

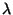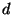NOTE: In this problem, please keep $\lambda$ and $d$ as variables - do not use the values given in problem 2!

(b)

Repeating part (a), find the phase difference between wave 0 and all the other waves seen by the observer (wave 2, wave 3, 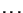$\ldots$, wave $N-1$.)

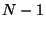(c)

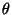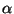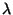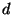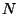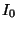Find the intensity measured by the observer as a function of $\theta$. (Your answer can also contain $\alpha$, $\lambda$, $d$, $N$, and $I_0$ - the intensity the observer would have measured if there were only a single reflecting groove.)

(d)

Sketch the interference pattern, $I(\sin\theta)$. Explain in a brief sentence or two how this pattern differs from the previously studied case, $\alpha=0$.

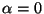Figure: Off-axis interference with a reflection grating.