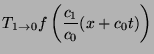


Next: About this document ...
Up: Reflection and transmission at
Previous: Final form for general
Contents
From the final general solution (16), it is relatively easy to
determine particular solutions for when a single pulse is incident
either from Region 0 or Region 1, thereby confirming the
interpretations giving in Section 3.3.3. For instance, if a
pulse of shape 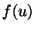 comes in from Region 0, then
comes in from Region 0, then 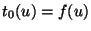 and
and
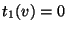 . Thus,
. Thus,
Thus, we have a reflected pulse, horizontally flipped and vertically
scaled by
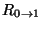 , traveling to the left in Region 0
with speed
, traveling to the left in Region 0
with speed 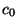 , and we have a transmitted pulse, stretched horizontally by
, and we have a transmitted pulse, stretched horizontally by
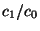 and scaled vertically by
and scaled vertically by
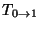 , traveling to
the right in Region 1 at speed
, traveling to
the right in Region 1 at speed 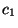 . Alternately, if a pulse of shape
. Alternately, if a pulse of shape 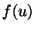 comes in
from Region 1, then
comes in
from Region 1, then 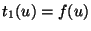 and
and 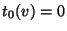 , and
, and
In this case, we then have a reflected pulse, horizontally flipped and
vertically scaled by
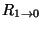 , traveling to the right in
Region 1 at speed
, traveling to the right in
Region 1 at speed 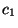 , and a transmitted pulse, horizontally
stretched out by a factor
, and a transmitted pulse, horizontally
stretched out by a factor 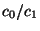 and vertically scaled by
and vertically scaled by
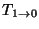 , traveling to the left in Region 0 at speed
, traveling to the left in Region 0 at speed  .
.



Next: About this document ...
Up: Reflection and transmission at
Previous: Final form for general
Contents
Tomas Arias
2003-10-26
![]() comes in from Region 0, then
comes in from Region 0, then ![]() and
and
![]() . Thus,
. Thus,