Interpretations

Eqs. (10,11) give all the information about the ``away' traveling functions. If, for instance, we wanted to know the value $a_0(3\mbox{\,{\bf m}})$, we could look at (10) at time $t=(3\mbox{\,{\bf m}})/c_0$, to find that

$$\begin{eqnarray*} a_0(3\mbox{\,{\bf m}}) & = & \frac{Z_0-Z_1}{Z_0+Z_1} t_0\left... ...1} t_1\left(\frac{c_1}{c_0} \cdot 3 \mbox{\,{\bf m}}\right). \\ \end{eqnarray*}$$

In more general terms, if we wanted to learn something about the value of $a_0(u)$ for any point $u$, we would look at (10) at the time $t=u/c_0$, to find

$$a_0(u) = \frac{Z_0-Z_1}{Z_0+Z_1} t_0(-u) + \frac{2 Z_1}{Z_0+Z_1} t_1( \frac{c_1}{c_0} u).$$ (12)

Note that this analysis corresponds precisely to the mathematical ``trick'' introduced in lecture of defining $u=c_0 t$. Following the same logic, to find the value of $a_1(v)$ for any point $v$, we should look at time $t=-v/c_1$ to learn from (11) that

$$a_1(v) = \frac{Z_1-Z_0}{Z_0+Z_1} t_1(-v) + \frac{2 Z_0}{Z_0+Z_1} t_0(\frac{c_0}{c_1} v).$$ (13)

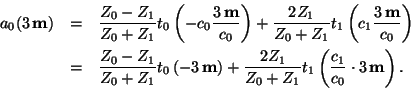
To interpret the results (12-13),⁶ we note that the pulse $a_0$ ($a_1$) traveling away from the interface into Region 0 (Region 1) has two contributions. The first comes from $t_0$ ($t_1$), the pulse originally traveling in Region 0 (Region 1) toward the interface, which evidently has been reflected by the interface back into Region 0 (Region 1). The ``$-u$'' (``-v'') in the argument of this pulse tells us that the reflected pulse is flipped horizontally, corresponding to the physical observation that the leading edge of a pulse should be the first part that returns in a reflection. The reflected pulse is also scaled vertically by a ``reflection amplitude'' which we denote $R_{0 \rightarrow 1}=(Z_0-Z_1)/(Z_0+Z_1)$ ( $R_{1 \rightarrow 0}=(Z_1-Z_0)/(Z_0+Z_1)$) to indicate reflection of a pulse traveling from Region 0 toward Region 1 (from Region 1 toward Region 0).

The second contribution to $a_0$ ($a_1$) comes from the pulse $t_1$ ($t_0$) originally traveling in Region 1 (Region 0) toward the interface, which is evidently then transmitted into Region 0 (Region 1). The ``$(c_1/c_0) u$'' (``$(c_0/c_1) v$'') in the argument of this pulse tells us that the transmitted pulse is horizontally stretched out by a factor of $c_0/c_1$ ($c_1/c_0$). This corresponds to the physical observation that a pulse entering a region of higher wave speed will be stretched out as the leading edge of the pulse rushes ahead into the new region where the waves move faster. Finally, the transmitted pulse is scaled vertically by a ``transmission amplitude'' for pulses which we shall denote $T_{1 \rightarrow 0}=(2 Z_1)/(Z_0+Z_1)$ ( $T_{0 \rightarrow 1}=(2 Z_0)/(Z_0+Z_1)$) to indicate transmission of a pulse from Region 1 into Region 0 (from Region 0 into Region 1),

The primary lessons of the above two paragraphs are that, in traveling from medium a to medium b, regardless of whether travel is from left to right or from right to left, reflected pulses always flip horizontally, and transmitted pulses always stretch horizontally by a factor $c_b/c_a$, where $c_a$ and $c_b$ are the respective wave speeds. (Note that, the pulse is actually compressed if this factor is a number less than one, like 0.8.) Moreover, reflected pulses scale vertically by a reflection amplitude

$$R_{a \rightarrow b} = \frac{Z_a-Z_b}{Z_a+Z_b},$$ (14)

and transmitted pulses scale vertically by a transmission amplitude

$$T_{a \rightarrow b} = \frac{2 Z_a}{Z_a+Z_b},$$ (15)

where $Z_a$ and $Z_b$ are the impedances of the respective materials.