


Next: Interpretations
Up: General Solution
Previous: Solution within each region
Contents
Substituting (4) into the consistency boundary
condition (1) gives,
where we have used the fact that (1) applies only at
the membrane point 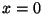 . This gives one equation for the four
adjustable functions, with which we could eliminate one function,
leaving three adjustable functions. We thus require only one more
relation among the four unknown functions.
. This gives one equation for the four
adjustable functions, with which we could eliminate one function,
leaving three adjustable functions. We thus require only one more
relation among the four unknown functions.
To generate this relation, we next substitute (4) into
the force balance boundary condition (3),
where 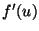 indicates the derivative of the function
indicates the derivative of the function 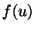 with
respect to its argument. We now have one additional equation, but
have introduced four additional functions, the derivatives
with
respect to its argument. We now have one additional equation, but
have introduced four additional functions, the derivatives 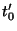 ,
,
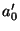 ,
, 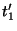 , and
, and 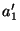 . This leaves us in the undesirable position of
having two equations in eight unknown functions. But, if we
integrate both sides of (6) with respect to time, we
can eliminate the derivatives, and have the second equation which we
need among just the original four adjustable functions. To integrate, we
guess at the result, check our guess by taking the derivative, and
then insert constants as needed to make the result match the original
equation. This procedure gives
. This leaves us in the undesirable position of
having two equations in eight unknown functions. But, if we
integrate both sides of (6) with respect to time, we
can eliminate the derivatives, and have the second equation which we
need among just the original four adjustable functions. To integrate, we
guess at the result, check our guess by taking the derivative, and
then insert constants as needed to make the result match the original
equation. This procedure gives
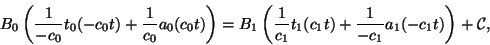 |
(7) |
where 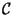 is the constant of integration and the factors
is the constant of integration and the factors
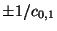 have been inserted to ensure that the derivative of
(7) with respect to time is precisely
(6). To determine the value of the integration
constant, we consider what happens before any waves are introduced,
have been inserted to ensure that the derivative of
(7) with respect to time is precisely
(6). To determine the value of the integration
constant, we consider what happens before any waves are introduced,
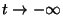 . For pulses of finite width,
. For pulses of finite width,
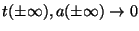 . Thus, the integration constant
above must be
. Thus, the integration constant
above must be
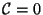 , and we may ignore it safely.
, and we may ignore it safely.
As a final simplification, we note that we can write both sides in
terms of the combinations of constants
Because this combination of constants appears so frequently in the
study of waves, it has a special name, the impedance. Because
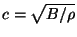 , the impedance is often written in the equivalent
form
, the impedance is often written in the equivalent
form
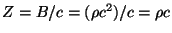 .5 With these definitions, we then rewrite (7) compactly
as
.5 With these definitions, we then rewrite (7) compactly
as
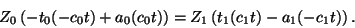 |
(9) |
Finally, we can use the two equations (5) and
(9) to eliminate two of the adjustable functions.
Because, as mentioned above, we generally study what comes out
from the boundary given what goes into it, the standard choice is
to use the boundary conditions to solve for the two ``away'' functions
in terms of the two ``toward'' functions. To solve for 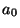 , we
choose a linear combination of (5) and
(9) which eliminates
, we
choose a linear combination of (5) and
(9) which eliminates 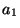 ,
,
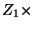 (5)
(5)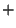 (9):
(9):
Similarly, to find 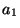 , we take the linear combination which
eliminates
, we take the linear combination which
eliminates 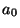 ,
, 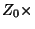 (5)
(5) (9):
(9):



Next: Interpretations
Up: General Solution
Previous: Solution within each region
Contents
Tomas Arias
2003-10-26
![]() , we
choose a linear combination of (5) and
(9) which eliminates
, we
choose a linear combination of (5) and
(9) which eliminates ![]() ,
,
![]() (5)
(5)![]() (9):
(9):