To find the general solution to the wave equation, we first prove an important lemma which has many useful applications in the theory of waves, the principle of superposition. Much like the principle of superposition which you learned in your introductory course on E&M, this principle allows us to quickly solve complex problems by breaking them into smaller parts for which we know the solutions.
Principle of superposition of waves -- If,
, ...all solve the wave equation, then the sum
is another valid solution.
Proof: To verify that y(x,t) is a solution, we compute
and check whether it indeed equals 
. During our computation, we are allowed to
use the facts that
,
, ...,
because the assumption of the lemma is that 
, 
, ..., are
all solutions. The result is
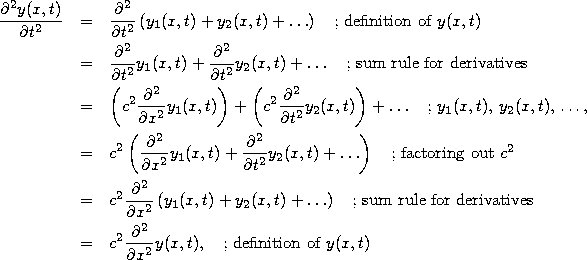
and so y(x,t) indeed solves the wave equation.
To find a general solution to the wave equation, we note that
the solutions to the pulse equation 
both automatically
solve the wave equation
, but each only has one
adjustable parameter for each degree of freedom. The wave equation is
second-order in time and therefore requires two adjustable
parameters for each degree of freedom. Thus, although each general
solution to the pulse equation has insufficient adjustable parameters
to be a general solution to the wave equation, by superposing two pulses,
one left-ward and one right-ward,
we are guaranteed to have a general solution to the wave equation. First, by superposition, we know we have a solution. Second, we will then have two adjustable parameters for each degree of freedom, one value of f(x) and one value of g(x) for each value of x.
