We now consider what sorts of functions satisfy the pulse equation.
Apart from the factor of 
, the pulse equation
(2) says that the t-derivative of q(x,t) gives
exactly the same result as the x-derivative. A good guess for a
solution is some function of x+t because then, when we apply the
chain rule, we will get the same function back times either
or 
of (x+t), which are
both just one. Actually, however, the pulse equation says that we
want the time derivative to give back an extra factor of .
Thus, a guess for a very general type of solution to the pulse
equation would be
where f() is any function whatsoever!
To verify the above as a solution, we take the appropriate derivatives and check the pulse equation (2),
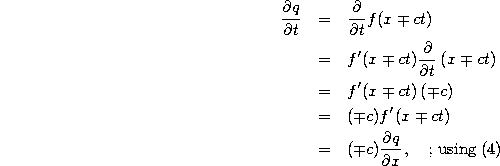
which proves that our form (3) for q(x,t) indeed solves (2). Moreover, because of our discussion in Section 2, we know that these solutions also solve the wave equation!
To interpret these solutions, consider Figure 1.
Figure 1a shows the solution at time t=0, which is
just a picture of the function f() because 
. Figure 1b shows the solution for the ``-''
version of the pulse equation at some time t later: 
, where we have defined 
. As the
picture illustrates, this is just exactly the same shape but shifted
to the right
by the distance a=ct. Similarly,
Figure 1c shows the solution for the ``+'' version of
the equation at some time t later: 
, where we again have defined , which is just
the same shape but shifted rigidly to the left by a=ct. Thus, our
solutions to the the ``-'' and ``+'' versions of the pulse
equation represent pulses, shapes which shift rigidly to the
right or left, respectively, with constant speed v=a/t=(ct)/t=c.
This is precisely why we have always referred to c as the wave
speed and why we refer to (2) as the left/right pulse
equations.
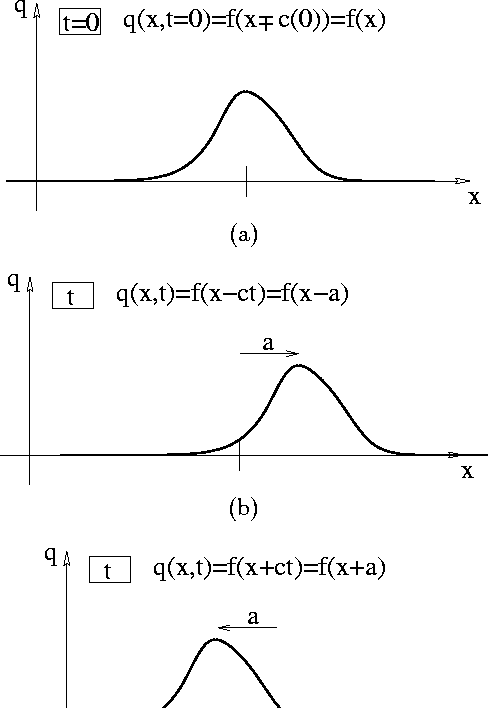
Figure 1: Time evolution of solutions to the pulse equations: (a) solution
at t=0, (b) right-ward or ``-'' solution at time t>0,
(c) left-ward or ``+'' solution at time t>0.
Given that our solutions (3) to the left/right pulse equations are in terms of a completely undetermined function f(), they are indeed quite general. But, are they truly general solutions? As discussed in Class Notes I, `` `Simple Harmonic' Motion (SHM),'' a general solution not only solves the equation of motion, but also does so with a number of adjustable parameters (unspecified constants which may take any value) equal to one for each order of time derivative appearing for each degree of freedom. The equation of motion for the simple harmonic oscillator was second-order in time, and therefore the general solution requires two adjustable parameters for each degree of freedom. As there is only one degree of freedom, ``x'', the general solution for the simple harmonic oscillator has two adjustable parameters.
The pulse equations, on the other hand, are first-order in time. Therefore, a general solution must have one adjustable parameter for each degree of freedom. In the pulse equations, as in the wave equation, the degrees of freedom are the values q(x) which specify the configuration of the system (position of a string, displacement of the air, value of the electric field, etc.) at any given instant in time. Now, q(x), which could be any function of x, actually specifies a large number of values, one value of q for each value of x. There is therefore one degree of freedom for each point x. Correspondingly, for a general solution, we need one adjustable parameter for each point x. Note that we emphasized that f() in (3) could be any function whatsoever. This means that we can pick any value of f(x) for each point x and still have a solution. The values f(x) for each x are, therefore, adjustable, and we have precisely one adjustable parameter, the value f(x) for each x, for each degree of freedom. The general solutions to (2) are therefore (3).
