To find a general solution to an equation such as (1), it generally behooves us to simplify it first. The wave equation (1) appears as though it could be simplified by taking its ``square root.'' In solving any kind of equation, we certainly always are allowed to take a guess at a simplification, so long as we check that it is correct in the end. Our guess at a ``square root'' is the following equation, which we shall call the pulse equation,
Note that in taking the ``square root'', we have been careful to include both possible choices of sign so that there are really two pulse equations, one for each sign.
To check that we have made a proper simplification, we now verify that any solution to either pulse equation (either the ``-'' or the ``+'' version) is also guaranteed to solve the wave equation. To do this, we are allowed to assume at each step that we satisfy the pulse equation (2) and try to prove that q satisfies the wave equation (1):
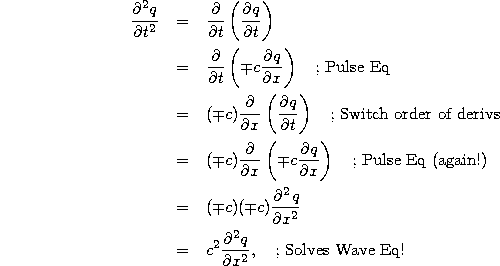
where we have used the fact that (-1)(-1)=(1)(1)=1. The fact that we were able to prove that q(x,t) solves the wave equation by assuming only that it solves either pulse equation means that, indeed, if we ever have a solution to the pulse equation we know also automatically that it solves the wave equation!