This section focuses on a very useful algebraic simplification we can
make to analyze interference patterns. The main lesson is that the
intensity at point 
is just 
, where
is the intensity that slit n would give if it were the only
slit, 
is the distance from slit n to the observation point, and
is the phase of the waves as they just emerge from slit n.
In fact, if you know just this result, you can derive the intensity
for any pattern of slits!
To understand this shortcut, we begin with
Eqs. 4 & 5, which tell us that the solution coming
from the 
slit, 
, arriving at point on
the screen is
with
The combined solution, therefore, will be
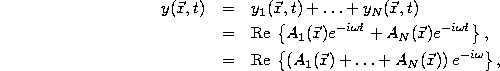
which is just simple harmonic motion with a complex amplitude which is the sum of each of the complex amplitudes,
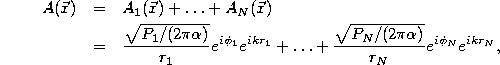
where we have used Eq. 7.
We can simplify our work dramatically if we now express everything in
terms of the intensities that we would see from each slit if it were
the only slit (Eq. 6), 
. To do
this, note that 
.
Thus,
Finally, even the factors of 
disappear when we compute the
intensity from all of the slits combined,
which is the simple result we gave at the start of this section. Note that most of this section has been managing algebra to get unknown constant factors to cancel out of the final expression, Eq. 8.
