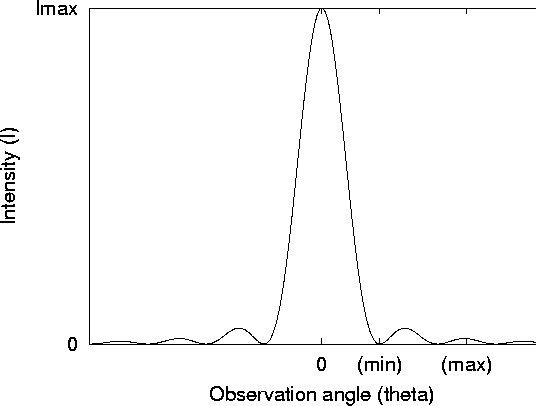
Figure 9: Intensity as a function of observation angle for a finite-slit experiment
Figure 9 shows an example of a diffraction pattern from a single slit. Again, several features are noteworthy.

Figure 9: Intensity as a function of observation angle for a
finite-slit experiment
![]()
This corresponds to ![]() , a path difference between one end of the
slit and the other of any non-zero integer number of wavelengths. If
the path difference is zero, all the contributions interference
constructively, and you get a large maximum. If the path difference
is not zero, but an even number of wavelengths, then we see that you
always find exactly canceling negative and positive contributions
from difference regions of the slit, leading ultimately to a minimum.
, a path difference between one end of the
slit and the other of any non-zero integer number of wavelengths. If
the path difference is zero, all the contributions interference
constructively, and you get a large maximum. If the path difference
is not zero, but an even number of wavelengths, then we see that you
always find exactly canceling negative and positive contributions
from difference regions of the slit, leading ultimately to a minimum.