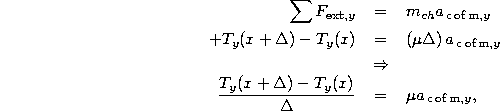
The y-component of (5) gives
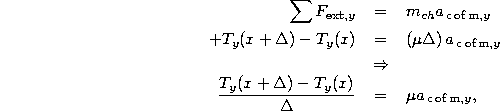
where we have divided through by 
, making the left-hand side
appear like a derivative. It is now quite natural to consider the
limit 
. In this limit, the left-hand side
approaches the partial derivative 
. (The
derivative is partial because we consider the two tensions at the same
instant in time and only x varies in taking the difference.) As we
take the the limit and shrink the segment to
the point x, the acceleration of the center of mass of the segment
becomes the same as the acceleration of the point at location x.
This acceleration then becomes the second partial time derivative of
the y-location of the segment at location x, 
. Combining
these limiting results we have
which makes the physical statement that for each tiny segment, it is the difference in the y-components of the tension which generates the acceleration.
There is a second, quite physical way to view (8). The
net force on a system gives the time rate of change of its momentum.
Because of Newton's third law of equal but opposite reaction forces,
force gives the flow of momentum from one part of a system to another.
The derivative 
thus gives the
difference between the momentum flowing into a small chunk and the
momentum flowing out. Thus should equal the time rate of change of
the momentum of the chunk 
, where we have defined the momentum per unit length (
momentum density) as
This quantity then allows us to rewrite (8) as
Turning back to the problem of finding a valid equation of motion, we
must express all quantities in terms of specified constants and
the solution y(x,t). The one quantity remaining in (8)
not yet in this form is the y-component of the tension 
. To
determine this component in terms of known quantities, we relate
to the known value of 
and the tangent of the angle of the
line of action of the tension relative to the horizontal ( 
in
Figure 2. The slope of the string at any instant in time
gives the tangent of this angle. Thus,
An equation such as this which relates the basic driving forces in a
system ( in this case) to the degrees of freedom is known
generally as the constitutive relation.
Finally, substituting the result (11) for the tension into the y-component of Newton's law (8), we have the equation of motion,
The equation of motion which we have found for the string (12) is precisely of the form of the famous wave equation,
where 
is some positive constant, which in the case of waves on a
string has the value
The next section explores some solutions for the wave equation and determines the meaning of the mysterious constant c appearing in the wave equation.
