The passage of a wave through any of the above systems disturbs, or moves,
all of the particles making up the gas, fluid or solid. As with the
string, the degrees of freedom must give some way to find the
locations of each chunk making up the system. For the case of sound,
we shall describe the disturbance by a vector 
which
gives the displacement of the chunk which started at location
when the system was at rest. Because gives
the displacement, if we wish to know the new location 
of the
chunk which started at , we compute it by adding the
displacement,
(See Figure 1.)
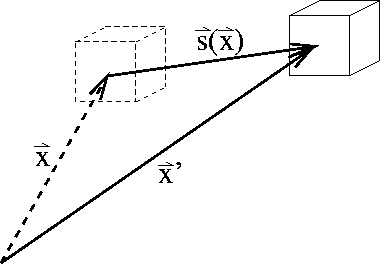
Figure 1: Mathematical description of disturbance in a sound wave:
initial position of chunk with system at rest ( ), final position of
chunk ( ), displacement of chunk initially located at
( ).
A solution for the sound wave, then would be a function 
giving the displacement of each chunk for all times
t. The location of each chunk at any time t is then
The velocity and acceleration of the chunk which starts at
location are, respectively,
where we have used the fact that, by the very definition of partial
derivative, 
.
