The equation of motion
expresses the controlling physical laws in terms of nothing other than
the degrees of freedom, derivatives of the degrees of freedom and
given physical quantities and constants. As for the physical laws,
the problem involves various types of energy, whose definitions we
must invoke, and also involves the quantum mechanical behavior of
particles, which the de Broglie hypothesis describes. Thus, we can
express the basic physical laws as
where we have been cautious to note that the presence of the force
means that the particle will have different velocities and thus
different momenta 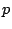 and wave vectors
and wave vectors 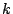 at each point
at each point 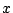 . This
equation expresses all of the physical laws in a single equation;
however, it uses
. This
equation expresses all of the physical laws in a single equation;
however, it uses  which, unlike all other quantities in the
equation, is not a given quantity. To complete the equation of
motion, we must find a way to express the wave vector directly in
terms of the degrees of freedom
which, unlike all other quantities in the
equation, is not a given quantity. To complete the equation of
motion, we must find a way to express the wave vector directly in
terms of the degrees of freedom 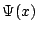 at its derivatives.
at its derivatives.
To find such an expression, first recall that the wave vector 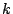 counts up how many oscillations there are in
counts up how many oscillations there are in 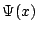 per unit
length. This kind of counting is difficult to express in terms of the
value of
per unit
length. This kind of counting is difficult to express in terms of the
value of 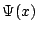 and its derivatives. However, the number of
oscillations per unit length is certainly related to the curvature of
and its derivatives. However, the number of
oscillations per unit length is certainly related to the curvature of
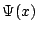 - the more curvature, the more oscillations per unit
length. To see this mathematically, consider the second derivative
(which gives the curvature) of any pure sinusoidal wave of arbitrary
amplitude and phase,
- the more curvature, the more oscillations per unit
length. To see this mathematically, consider the second derivative
(which gives the curvature) of any pure sinusoidal wave of arbitrary
amplitude and phase,
Thus, we see that we can get a measure of the wave vector 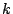 at any
point by looking at the ratio of the second derivative to the value of
the function,
at any
point by looking at the ratio of the second derivative to the value of
the function,
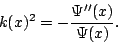 |
(17) |
Substituting the result Eq. (17) into Eq. (16)
gives the final equation of motion,
Or, equivalently,
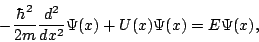 |
(18) |
where in the last line we have rearranged things somewhat to
correspond to the standard way of writing the quantum equation of motion, the
famous Schrödinger
Equation.
Tomas Arias
2004-11-30
![]() counts up how many oscillations there are in
counts up how many oscillations there are in ![]() per unit
length. This kind of counting is difficult to express in terms of the
value of
per unit
length. This kind of counting is difficult to express in terms of the
value of ![]() and its derivatives. However, the number of
oscillations per unit length is certainly related to the curvature of
and its derivatives. However, the number of
oscillations per unit length is certainly related to the curvature of
![]() - the more curvature, the more oscillations per unit
length. To see this mathematically, consider the second derivative
(which gives the curvature) of any pure sinusoidal wave of arbitrary
amplitude and phase,
- the more curvature, the more oscillations per unit
length. To see this mathematically, consider the second derivative
(which gives the curvature) of any pure sinusoidal wave of arbitrary
amplitude and phase,
