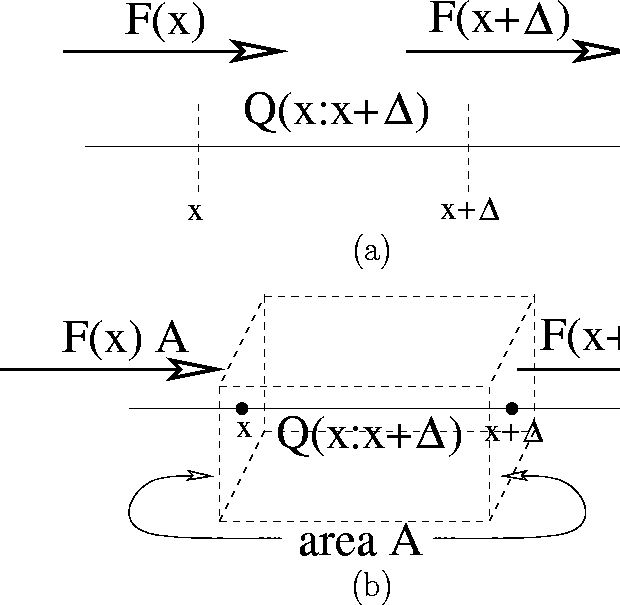
Figure 1: Conservation of quantity Q stored between points x and
The general continuity equation accounts for the conservation of any quantity Q which may be flowing in a system in terms of the density of that quantity at all points q(x) and the rate of flow of the quantity F(x) from left-to-right from one point to the next.

Figure 1: Conservation of quantity Q stored between points x and
![]() in terms of in-flow and out-flux F(x): (a) in d=1
dimension, and (b) in d=3 dimensions.
in terms of in-flow and out-flux F(x): (a) in d=1
dimension, and (b) in d=3 dimensions.
If we indeed Q is conserved while flowing from point to neighboring
point, then the rate of change in the amount of Q between points x
and ![]() comes only from flow at points x and
comes only from flow at points x and ![]() , as
Figure 1 illustrates.
, as
Figure 1 illustrates.
The mathematical definitions of the relevant quantities depend upon
the dimensionality of the system. If we describe a d=1 dimensional system
(Figure 1a), then we define the density q as the linear
density, the amount of quantity Q per unit length, and the
flow F(x) as the rate of flow of Q across the point x. By
convention, we define flow from left to right
as positive. Then, if ![]() is the amount of
quantity Q between points x and
is the amount of
quantity Q between points x and ![]() , we have a contribution
flowing in at point x at a rate of +F(x), and a contributing
flowing out at point
, we have a contribution
flowing in at point x at a rate of +F(x), and a contributing
flowing out at point ![]() at a rate
at a rate ![]() . (See
Figure.) Thus,
. (See
Figure.) Thus,
expresses conservation of Q in between points x and ![]() .
.
A more useful expression of the same idea is one in differential form.
To find this, we divide (1) through by ![]() ,
rearrange the order of terms on the right-hand side, and take the
limit
,
rearrange the order of terms on the right-hand side, and take the
limit ![]() . This gives
. This gives
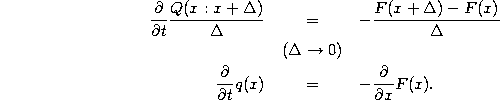
Hence,
If, on the other hand, we have a d=3 dimensional system (Figure 1b), we then define the density q as the volume density, the amount of quantity Q per unit volume, and the flow F as the rate of flow per unit area of quantity Q. Following a similar analysis, we will now find that, under these definitions, the same mathematical expression applies also in d=3 dimensions. Note that we continue to assume plane-wave behavior so that the basic system quantities depend only upon x.
To carry out the analysis, we now define ![]() as the
amount of the quantity in the box of cross-sectional area A
extending from point x to point
as the
amount of the quantity in the box of cross-sectional area A
extending from point x to point ![]() . The net rate of flow
into the box across the face at point x is now F(x) A and
the flow out of the box across the face at
. The net rate of flow
into the box across the face at point x is now F(x) A and
the flow out of the box across the face at ![]() is
is
![]() . Thus,
. Thus,
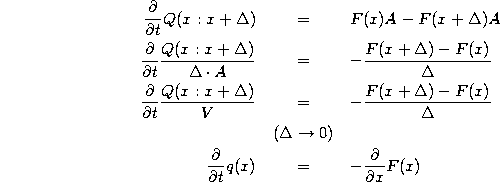
Hence, we again find the same equation, but with the quantities now defined as appropriate for a d=3 dimensional system,
The identical equations (2,3) are known as The Continuity Equation for quantity Q. They apply for any quantity which is conserved and which moves by flowing from one point to the neighboring point. We now consider whether momentum and energy can be described in this way.