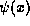 for a system in the position
representation and we wish to compute the average position of the
particle after many measurements. Within the framework we have
established so far (provided that
for a system in the position
representation and we wish to compute the average position of the
particle after many measurements. Within the framework we have
established so far (provided that 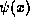 is properly normalized), we
would compute simply
is properly normalized), we
would compute simply
We shall begin with the calculation of the average observed position
of a particle. Suppose that we are given the
wave function, or quantum amplitudes, 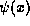 for a system in the position
representation and we wish to compute the average position of the
particle after many measurements. Within the framework we have
established so far (provided that
for a system in the position
representation and we wish to compute the average position of the
particle after many measurements. Within the framework we have
established so far (provided that 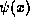 is properly normalized), we
would compute simply
is properly normalized), we
would compute simply
This is a perfectly valid form for computing averages of x; but because it depends so much on the position representation, it is not convenient to work with if we desire a very general framework for computing averages, one which we may use no matter in which representation we are working.
As we have already seen from Parseval's theorem, however, we may write
integrals in a representation-independent manner by writing them
as Hermitian inner products 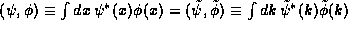 . Accordingly, a much better way to write
(1) is as
. Accordingly, a much better way to write
(1) is as
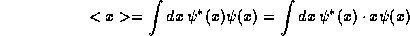
This is clearly the same form as (1). But, now if we
had been working in the momentum representation and wanted to compute
<x>, instead of first doing the Fourier integral
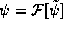 to find
to find 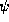 and then using (1), we
may now immediately apply Parseval's theorem to (2)
and then using (1), we
may now immediately apply Parseval's theorem to (2)
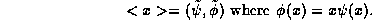
Note that
here we have the same mathematical structure as (2),
<x> is given by the inner product of the wave function (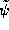 )
with some other function (
)
with some other function (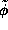 ) which is derived from the wave
function through some well-defined procedure. In (2)
the ``procedure'' is simply to multiply by x, the argument of the
wave function in the representation. Here, the ``procedure'' is more
complicated and involves three phases. We begin with
) which is derived from the wave
function through some well-defined procedure. In (2)
the ``procedure'' is simply to multiply by x, the argument of the
wave function in the representation. Here, the ``procedure'' is more
complicated and involves three phases. We begin with 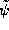 and 1)
Fourier transform it to obtain
and 1)
Fourier transform it to obtain 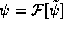 . We then 2) multiply
by x to get
. We then 2) multiply
by x to get 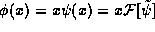 . Finally, 3) we inverse
Fourier transform back to get
. Finally, 3) we inverse
Fourier transform back to get 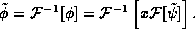 Fortunately, the effect of this entire complex
procedure on the function
Fortunately, the effect of this entire complex
procedure on the function 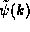 is very simple,
is very simple,
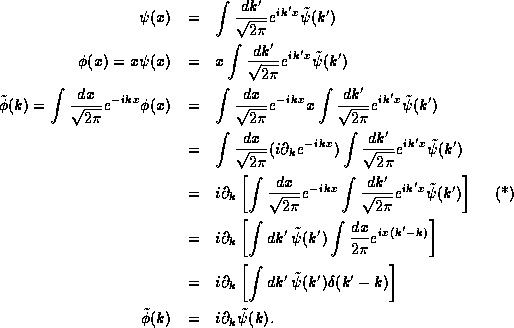
In step (*) we used the fact that only the 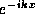 term depends on
k in order to pull the derivative
term depends on
k in order to pull the derivative 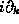 out of the
integral. After writing (*) we could have recognized that the
expression inside the square brackets is the expression to transform
out of the
integral. After writing (*) we could have recognized that the
expression inside the square brackets is the expression to transform
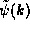 and then inverse transform the result, which then just
returns
and then inverse transform the result, which then just
returns 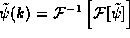 . We proceeded
directly, instead, to review for the student the use of the Dirac
. We proceeded
directly, instead, to review for the student the use of the Dirac
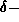 function.
function.
With 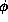 in hand, we now have two equivalent ways of writing
<x>, one for each representation,
in hand, we now have two equivalent ways of writing
<x>, one for each representation,
In both cases <x> is just given by the Hermitian inner product
of the wave function (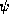 or
or 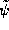 ) with some function derived
from the wave function through some mathematical procedure or
``operation''. As we shall see in section 3, this will
lead us to define ``function operators.'' First, however, we will
complete our discussion of averages with expressions for averages of
momentum, the other primary observable for this course.
) with some function derived
from the wave function through some mathematical procedure or
``operation''. As we shall see in section 3, this will
lead us to define ``function operators.'' First, however, we will
complete our discussion of averages with expressions for averages of
momentum, the other primary observable for this course.