
In each of the four cases presented in (3) and (4), we find that the average of an observable is computed as the inner product of the wave function with some other function derived from the wave function through some mathematical operation. We will see in section (4) that this structure for the calculation of averages is completely general in quantum mechanics.
In this section we will focus on the mathematics of operations performed on functions to produce other functions. We will call such an operation a function operator. A function operator is a generalization of our familiar notion of a function. We normally think of a function as a ``map'' which associates a single real number as output for every real number given to the function as input. However, there is nothing in the idea of a function that requires its input and output to be real numbers. They could be complex numbers or the input and output could be functions themselves. A function operator is then just a special case of this general notion of function. A function operator accepts functions as input, and maps each input function to a single unique function as output. We call these special functions ``function'' operators to remind us that as input and output, they accept and give functions rather than numbers. Later, in section (4) we shall define quantum operators, which map not functions but quantum states.
In analogy with the usual notation for the operation of a function f on a real number x

we introduce the following notation for the operation of an operator
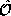 on a function
on a function 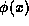 ,
,

The caret `` '' tells us that
'' tells us that 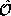 is a function operator
which acts on the function immediately to its right,
is a function operator
which acts on the function immediately to its right, 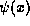 , giving
the result
, giving
the result 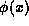 .
.