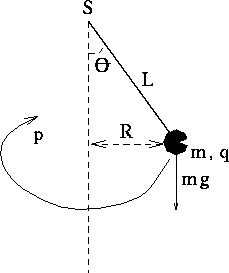
In this problem, you will analyze the consequences of the de Broglie
relations (i.e., Bohr quantization) on the motion of a ``conical
pendulum.'' A conical pendulum (see Figure 1) is very much like a
normal pendulum, there is a mass m suspended from a point S by a
rigid massless rod of length L and subject to the force of gravity
mg. In the case of the conical pendulum, the rod is free to move in
anyway about the point S so that it can make circular orbits of
radius R as indicated in the figure. For the purposes of this
problem we will also place, a small test charge q on the mass m.
For reference, we will call the momentum of the particle p, the
angle which the rod L makes with the direction of the vertical
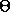, the distance from the mass m to the vertical line R, the
total energy (kinetic plus potential) of the pendulum E, and the
period when the particle undergoes circular motion T. In the Bohr
analysis of the motion there must be an integral number n of de Broglie
wavelengths around the circumference of the orbit of radius R.
In a quantum state n, there are specific values allowed to the angle
and energy of the system, which we shall call 
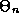, and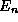 
,
respectively. Your task is to use the Bohr quantization
condition to compute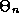 
and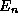 
, compare the lowest
state n=1 with the predictions of the Heisenberg Uncertainty
Principle, and understand the behavior of the level spacings in the
spectrum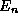 
by using the correspondence principle.
a) Intuitively, how to you expect the period of the conical
pendulum's motion to vary (increase or decrease) as its energy it
increased? Using the general result from the correspondence principle
given in class that in the classical limit, the level spacing is given
by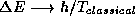 
, where 
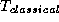is
the classical period of the motion, how do you expect the spacing
between the energy levels of the pendulum to vary (increase or
decrease) as its energy increases?
b) What is
the momentum p of the particle as a function of the
angle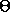 
of the pendulum as the particle moves in its circular
orbit? What is the period and total energy (kinetic
plus potential) of this motion? Express all three answers
in terms of just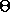 
, L, m and g.
c) If a small test charge q is placed on the mass m, what
frequency radiation would the pendulum emit when rotating in a circular
orbits at an angle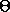 
?
d) Use the Bohr quantization condition that there must be an
integral number n of de Broglie wavelengths around the circumference
of the orbit of radius R, to find a condition on the
allowed quantized values of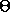 
, 
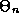in terms of the
quantum number n and the constants 
, m, g and L.
(Hint: To get an explicit form for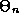 
you would have to solve
a ugly equation. Instead you may express your result in the
implicit form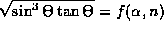 
where
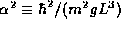and f is some function.
e) Check your result for d) by using the
uncertainty principle to to estimate the average angle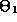 
in
the ground state of the pendulum. (For this part of the problem you
may assume that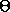 
is small so that 
.)
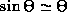f) Under the assumption that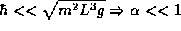 
(the classical limit), give an expression for the spacing
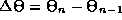between the allowed
quantized angles of the system in terms of 
and the classical
angle of the pendulum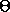 
. From your expression for 
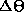, determine the spacing 
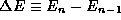between
neighboring energy levels in terms of the angle of the pendulum
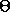. Do the spacings exhibit the behavior you predicted in a)?
g) Show explicitly that photons emitted by the
pendulum making a transitions between neighboring energy levels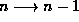 
represent precisely the same frequency
radiation expected in c).
