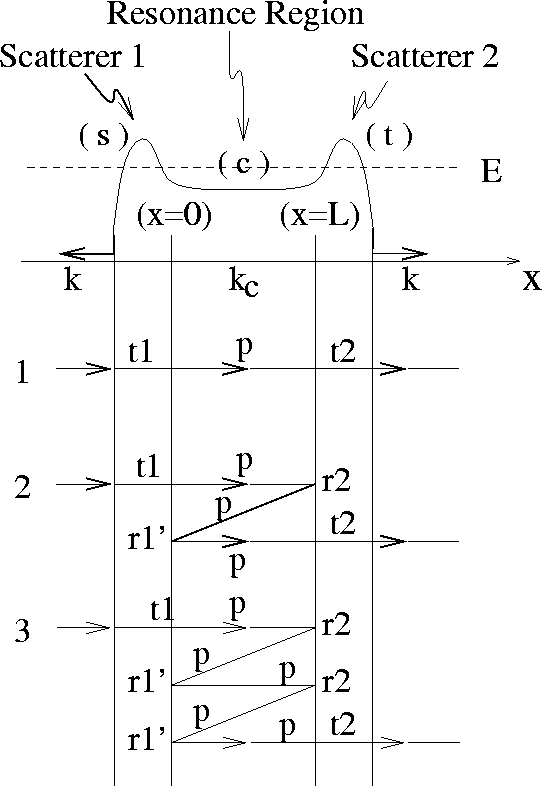
Figure 15: General Resonant Scatterer: two symmetric scatterers of width a separated by a propagating region of width L. Outside of the two scatterers, the potential is constant.
The Feynman rules at which we arrived in Section 3.5 are quite intuitive and we most likely could have guessed at them from the beginning based upon our physical intuition. The bulk of the discussion in Section 3 has been to demonstrate the equivalence of the Feynman and Schrödinger approaches for scattering in one dimension and to establish the Feynman rules. Once this is accomplished, it is a simple matter to draw out and label the diagrams in Figures 13 and 14. The final transmission and reflection amplitudes are then the sums over all the corresponding diagrams of the product of all of the labels. The result is precisely what we found in the Schrödinger formulation but now obtained in an extremely elegant and simple manner.
The raw power of the Feynman approach is illustrated by the fact that the sums (17) which we have derived are completely general. They are valid for any scattering potential made from two scattering centers, not merely the two equal but opposite steps which we originally had in mind. Figure 15 shows another example of a scattering potential involving two scattering centers made from the general barriers we studied in Section 3.2. As the figure shows, the quantum amplitudes for this far more complicated potential are described by precisely the same Feynman sum. The Feynman approach brings out the essential physics which this potential and the simple barrier share.

Figure 15: General Resonant Scatterer: two symmetric scatterers of
width a separated by a propagating region of width L. Outside of
the two scatterers, the potential is constant.
The sums (17) themselves are also rich in physical
structure which we may exploit in determining their values. Each term
in the transmission sum, for instance, involves transmission into the
barrier region ![]() , some number (possibly zero) of repetitions of the
basic ricochet sequence
, some number (possibly zero) of repetitions of the
basic ricochet sequence ![]() , and then a final propagation across
the scattering region and transmission out of the second scatterer
pt'. Organizing the sum according to this physical principle, we
find
, and then a final propagation across
the scattering region and transmission out of the second scatterer
pt'. Organizing the sum according to this physical principle, we
find
After factoring the common parts from the histories, we are left with an easily summed standard geometric series,
This factoring into common end-point events and a basic repeating
sequence is a common feature of most Feynman sums, even in far more
complicated contexts. A basic
repeating unit similar to the ricochet factor, for instance, appears
in field theory to represent the self-energy of the electron and
eventually leads to the theory of renormalization of the
electron mass. Note that there is no mathematical need to write the
ricochet factor as ![]() . We could just as well write
. We could just as well write ![]() . The former form, however, helps us to keep in mind the physical
origin of the term.
. The former form, however, helps us to keep in mind the physical
origin of the term.
The sum for reflection is only slightly more complex. The first term
is a different from the others because it is the only term which
involves reflection when approaching the first barrier from the left
( ![]() ). All of the other terms involve the processes needed to reach
the second barrier and reflect back from it and out the entire barrier
). All of the other terms involve the processes needed to reach
the second barrier and reflect back from it and out the entire barrier ![]() . These terms also may contain any number,
possibly zero, of ricochets between the two barriers (
. These terms also may contain any number,
possibly zero, of ricochets between the two barriers ( ![]() ).
Organized this way, the sum becomes
).
Organized this way, the sum becomes