As a specific example of resonance, consider the simple barrier
potential of Figure 1 with which we started. In this
case the spacing between the barriers is L=a. From
(15), the phase of r is 
and the transmission and
reflection probabilities are
respectively. According to (23) the final transmission probability is then
And, this is precisely what we would find by direct solution of the Time Independent Schrödinger Equation (TISE)!
In Figure 16, we plot the transmission amplitude 
as a
function of the momentum 
of the particle as it crosses the
collision region, for various values of the height of the potential
step 
. In the figure, 
, the kinetic energy
of a particle bound in an infinite square well potential of length
a, sets the energy scale. Perhaps the most striking result in the figure is that precisely
at the values 
, we find perfect probability for
transmission, 
. Also as expected, when becomes very
large, the presence of the barrier becomes less and less significant,
so that the transmission probability approaches unity at large
regardless of whether is at one of the resonances. As we
increase the height of the barrier, as we would expect, the
transmission probability for low values of decreases rapidly.
As a consequence, the resonances become very narrow, as
seen in the figure.
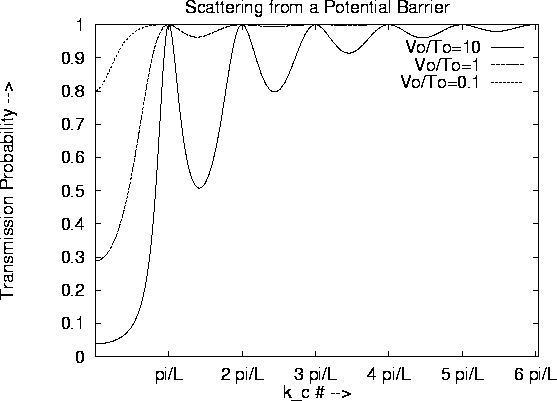
Figure 16: Transmission Probabilities across a square potential barrier
