Once it is understood that in special bands of energy electrons may propagate through an infinite crystal, it is natural to inquire as to what happens in a more realistic situation when there is disorder in the crystal, for instance when the spacing between the atoms is slightly irregular with small, random perturbations. Phil Anderson won the Nobel prize in 1977 for his investigations into this very issue.
Our renormalization approach to crystal propagation makes such studies
easy to carry out. We now compute the renormalization flows according to
(29) with a simple computer program which generates slightly
random displacements between the atoms and therefore slightly
different 
for each n. Figures
21.1-21.6 show the renormalization flows
of the transmission amplitude for a random crystal (with atomic
locations varying by 
%) at precisely corresponding energies
to those in Figure 20.
Figures 21.1,4,5 show the typical behavior in the gap. There is still a rapid approach to the origin, although now the approach is a little random. The electrons still cannot propagate at these energies in the gaps.
Figures 21.2,3,6 show that with disorder, even electrons in the allowed energy bands cannot propagate in the crystal. The flows cycle around the origin as before, but all eventually spiral into it. By studying how quickly these flows ``fall'' into the origin, one may determine the typical maximum distance which an electron may travel in the crystal. These results show that all electrons become localized in this random crystal, a phenomena known as Anderson localization.
The Anderson localization teaches us an important lesson about propagation in the crystal. The classical result for the transmission probability through a crystal of scatterers is that the final probability is the product of all of the probabilities of crossing the barriers. So long as the probability of crossing each scatterer is not exactly one, classical thinking predicts that in an infinite crystal the final transmission probability will be zero. What is different in the quantum analysis is that we now must sum complex amplitudes over all histories. In this sum in perfect crystals, at those energies in the allowed bands, there is enough constructive interference in the forward direction to allow the propagation to continue. By introducing randomness into the crystal, we disturb this constructive interference sufficiently to localize the electrons.
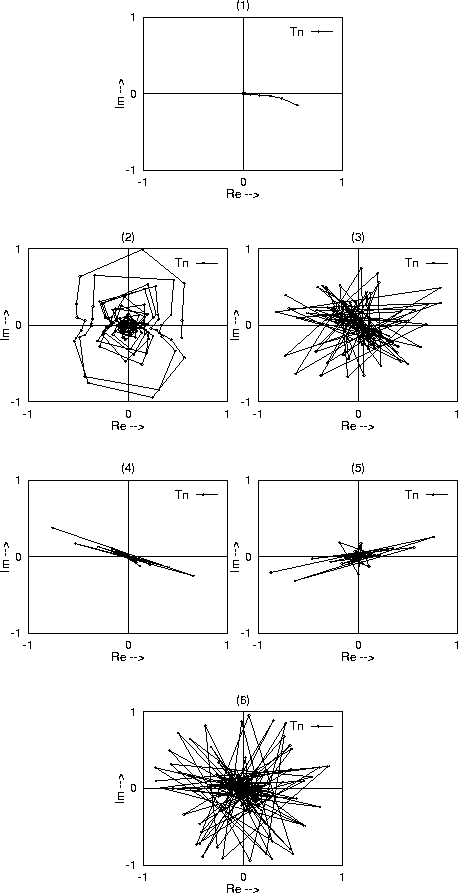
Figure 21: Renormalization Flows of Transmission Through Disordered Crystal