In Section 5.1 we showed how renormalization,
redefinition of fundamental processes into larger units, allowed us to
organize and perform the Feynman sum for a three scatterers. In this
section, we take the idea to the next level in order to analyze
scattering from a infinite perfectly periodic array of scatterers,
corresponding to the physics of electrons moving through a crystal.
(A crystal is a perfectly regular array of identical atoms, each of
which, by renormalization into a single unit, may be viewed as a
single scatterer.) For concreteness we will consider an infinite
array of 
functions but, again the Feynman approach will allow
us to derive general formulae which differ from system to system only
in the specific values assigned to the scattering amplitudes of the
fundamental units.
Figure 19 illustrates the potential which we consider. The infinite variety of Feynman diagrams describing electrons which are transmitted into the crystal and never return is so large that they are no longer countable, there are in fact as many of these diagrams as there are real numbers. We must be very clever in organizing the sum of these diagrams.
Figure 19: Renormalization Group Calculation of Propagation Through a Crystal
Our strategy here is to apply the idea of renormalization over and over and study the behavior of the system in the limit of an infinite number of renormalizations. Figure 19 illustrates how this process allows us to study an infinite crystal. Our strategy is to build upon the results of Section 5.1. We now take the quantum amplitudes for the first three scatterers taken together as a renormalized unit and combine this unit with the fourth scatterer to find the quantum amplitudes for the first four scatterers as a renormalized unit. We then combine this quadruple unit unit with the fifth scatterer in the sequence to produce the transmission amplitude for the first five. We continue the process to build up the amplitudes for an infinite crystal. The idea of applying successive renormalizations like this is known as the Renormalization Group. It represents the intellectual content of Ken Wilson's Nobel prize in 1982.
Specifically, at each step in the process, we take the
scattering amplitudes for the first n units 
and combine them with the quantum amplitudes for the next bare
scatterer in the sequence 
and
the propagation factor separating these two units 
. The
mathematics of this is
precisely the same as we followed to produce 
from
in
(26,27,28). The general result is
where the initial case is that 
as
indicated in Figure 19.
The behavior of a single physical quantity, such as the transmission
coefficient, as a function of the number of times the renormalization
is carried through is known as the renormalization flow of the
quantity. Figure 20.1 shows the renormalization flow of
in the complex plane for a small value of the incoming energy.
The first of the connected points on the plot, approximately 0.45-0.2
i, shows the value (25) for the transmission
amplitude across one function at this energy. The
transmission probability across one function at this energy
is therefore approximately 
. The successive
points on the plot show the transmission amplitudes across n
functions at this energy as computed according to
(29) with a very simple computer program. The plot shows that
as 
, 
and therefore these
electrons do not have enough energy to propagate through the crystal.
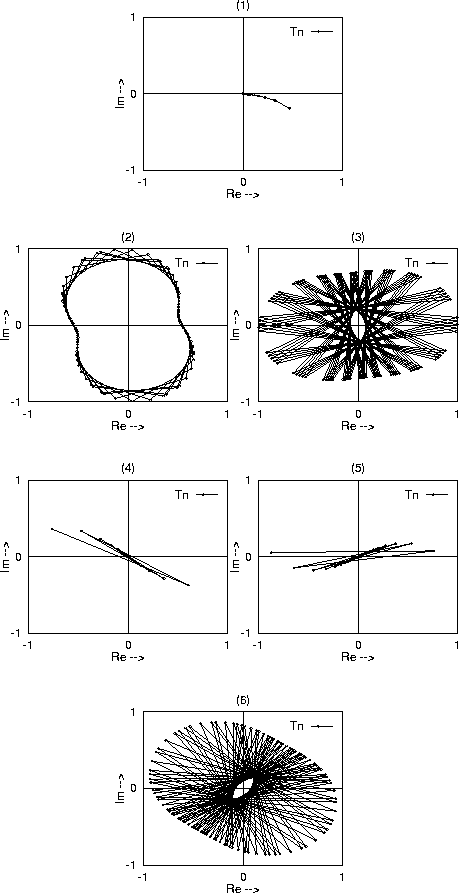
Figure 20: Renormalization Flows of Transmission Through a Perfect Crystal
Figure 20.2 shows the flow at a slightly higher value of
the energy. Now something interesting happens. As n increases, the
transmission amplitudes do not approach a limit. They cycle around in
the complex plane in a figure-eight pattern and never approach the
origin. These electrons may therefore propagate through the crystal
without returning. The fact that the transmission amplitudes do not
settle down to a single point indicates that the electronic wave
function is sensitive to the placement of the next atom in the
crystal, another indicator that the wave function for the electron
spreads throughout the entire crystal. As the energy is further
increased we see a continuous series of such patterns; one of the
highest energy ones appears in Figure 20.3. Such a
continuous range of energies where electrons may propagate in a
crystal is called an allowed band in solid state physics.
Note that for this state near the top of the band, the successive now appear on nearly opposite sides of the
origin. This indicates that the phase going through successive
functions is approaching -1.
As we continue to increase the energy we find the flow of Figure 20.4. The phases from successive scatterers are now sufficiently close to -1 that the successive reflections in the crystal no longer interfere sufficiently constructively to allow the electrons to propagate forward in the crystal. This continues as we increase the energy through that of Figure 20.5. A range like this where no states propagate through the crystal is known in solid state physics as a gap or band gap. Finally, Figure 20.6 shows that with a little more energy, we begin another band of energies where propagation occurs. This alternation between bands and gaps continues as we increase the energy of the electrons.
