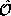The proof of Ehrenfest's theorem proceeds directly and in a similar
manner to the proof of the continuity equation: we begin with the
time derivatives in the statement we wish to prove and then replace
the time derivatives using the TDSE. The first part of the proof of
Ehrenfest's Theorem is very general. It applies to the time derivative
of the average of any physical observable and depends only on the TDSE
and the fact that the Hamiltonian operator, being associated with the
observable E, is always
Hermitian. We will give the general result for an arbitrary operator
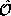first and then apply this result
to prove Ehrenfest's theorem.
The time derivative of the average of an observable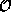 
will always obey
where by the average of an operator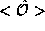 
in a state 
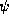we just mean the inner product 
.
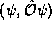Note that our development of (12) is completely
general and has used nothing other than the dynamics 
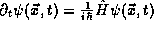from the
Schrödinger equation and the fact that the Hamiltonian, being
physical, is a Hermitian operator.
