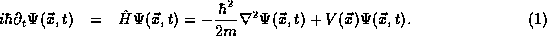
The time dependent Schrödinger equation in a three dimensional system reads
For a one dimensional system it becomes just
As in the previous note, although we shall focus for the most part of
this course on one dimensional systems, we shall carry
through the developments in this note for the more general case of
three dimensional systems which we will need when we study the hydrogen
atom. To recover the one dimensional results, you need only
remove the vector symbol ``
'' and replace 
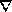with
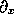in all of the equations below.
The method of the separation of
variables is most often applied in the case of linear partial
differential equations. We would like to emphasize at this point that
the TDSE is linear, which means that the sum of any two solutions
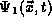and
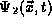to the equation gives a third valid solution
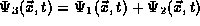. The student may verify
this easily by direct substitution of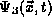 
into
(1).
Note that in the
equations below we have written the wave function,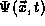 
as with an upper case letter 
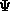. We do this because
momentarily we will separate the time and spatial dependencies of these
equations and derive a new equation, the TISE, describing a
time-independent wavefunction
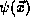which we will denote with a lower case 
.
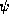