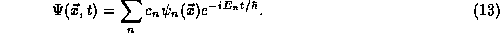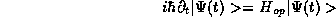Next: Properties of Solutions
Up: Separation of Variables
Previous: The separation procedure
The intriguing thing about the solutions 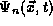 of the
previous section is that they
form a complete set, which means that
all valid solutions to (1) maybe made out of sums of
the particular solutions
of the
previous section is that they
form a complete set, which means that
all valid solutions to (1) maybe made out of sums of
the particular solutions 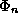 we have identified. This is a general
feature of the solutions generated by the procedure of the separation
of variables.
The proof of this as a mathematical statement
is beyond
the scope of this course. We can see, however, on physical grounds
that the solutions we have identified must be complete provided that we have
the correct mathematical representation of our pure physical
quantum states.
we have identified. This is a general
feature of the solutions generated by the procedure of the separation
of variables.
The proof of this as a mathematical statement
is beyond
the scope of this course. We can see, however, on physical grounds
that the solutions we have identified must be complete provided that we have
the correct mathematical representation of our pure physical
quantum states.
The physical reason for our confidence in the completeness of our
solutions comes from the very special form of equation
(9). It is just the eigenvalue equation for the energy
operator!
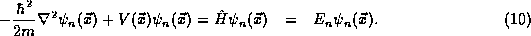
The 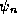 are eigenstates of the Hamiltonian operator
are eigenstates of the Hamiltonian operator 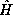 .
Each solution
.
Each solution 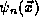 to this equation is a pure state of the
energy observable with energy
to this equation is a pure state of the
energy observable with energy 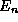 . The only values which may be
observed when the measure the energy of the system are the
. The only values which may be
observed when the measure the energy of the system are the 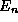 where
(10) has a valid solution. This is the reason for our choice of
the name E for the constant which appeared in our separation of
variables analysis.
where
(10) has a valid solution. This is the reason for our choice of
the name E for the constant which appeared in our separation of
variables analysis.
The completeness of our solutions may be understood through the
physical principle of superposition, which states that
we may write all quantum states at a given time t=0 as an
amplitude-weighted sum of the pure states of the physical observable
of the energy,
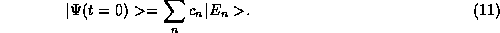
In the position representation, this means that
we may expand any
wavefunction
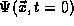 at time t=0 in terms of our solutions to the TISE
at time t=0 in terms of our solutions to the TISE
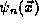 ,
,
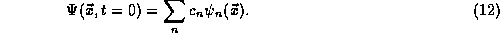
From our separation of variables, we do know that 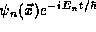 is a solution to the Time Dependent
Schrödinger Equation (1). Because the TDSE is
linear,
is a solution to the Time Dependent
Schrödinger Equation (1). Because the TDSE is
linear, 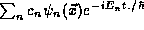 is also a solution. Because, as we saw
above, the
is also a solution. Because, as we saw
above, the 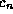 may be chosen so that
may be chosen so that 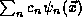 matches an arbitrary
matches an arbitrary 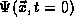 at t=0, the
general solution to the TDSE may be written
at t=0, the
general solution to the TDSE may be written
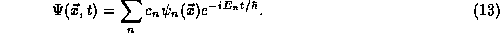
The interested student should note (and try as an exercise) that one
may go (in three or four lines of algebra!) from the more abstract
Schrödinger equation
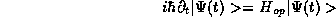
and the principle of superposition
(11) to derive almost immediately the central result
of this note (13).



Next: Properties of Solutions
Up: Separation of Variables
Previous: The separation procedure
Prof. Tomas Alberto Arias
Thu Oct 12 16:07:59 EDT 1995
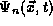 of the
previous section is that they
form a complete set, which means that
all valid solutions to (1) maybe made out of sums of
the particular solutions
of the
previous section is that they
form a complete set, which means that
all valid solutions to (1) maybe made out of sums of
the particular solutions 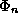 we have identified. This is a general
feature of the solutions generated by the procedure of the separation
of variables.
The proof of this as a mathematical statement
is beyond
the scope of this course. We can see, however, on physical grounds
that the solutions we have identified must be complete provided that we have
the correct mathematical representation of our pure physical
quantum states.
we have identified. This is a general
feature of the solutions generated by the procedure of the separation
of variables.
The proof of this as a mathematical statement
is beyond
the scope of this course. We can see, however, on physical grounds
that the solutions we have identified must be complete provided that we have
the correct mathematical representation of our pure physical
quantum states.
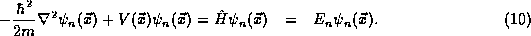
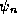 are eigenstates of the Hamiltonian operator
are eigenstates of the Hamiltonian operator 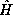 .
Each solution
.
Each solution 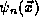 to this equation is a pure state of the
energy observable with energy
to this equation is a pure state of the
energy observable with energy 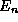 . The only values which may be
observed when the measure the energy of the system are the
. The only values which may be
observed when the measure the energy of the system are the 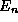 where
(
where
(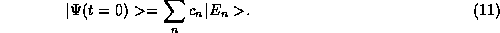
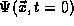 at time t=0 in terms of our solutions to the TISE
at time t=0 in terms of our solutions to the TISE
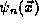 ,
,
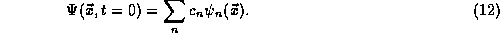
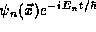 is a solution to the Time Dependent
Schrödinger Equation (
is a solution to the Time Dependent
Schrödinger Equation (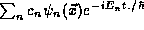 is also a solution. Because, as we saw
above, the
is also a solution. Because, as we saw
above, the 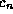 may be chosen so that
may be chosen so that 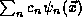 matches an arbitrary
matches an arbitrary 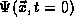 at t=0, the
general solution to the TDSE may be written
at t=0, the
general solution to the TDSE may be written