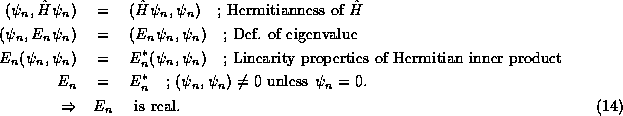Next: Orthogonality of the
Up: Properties of Solutions
Previous: Properties of Solutions
While from their physical interpretation as the eigenvalues of a
physical operator (10) and thus values observed
in physical measurements, it is clear on physical grounds that
the energy eigenvalues
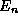 must be real. Nonetheless, it is as useful exercise and a simple
consistency check on our theory to verify mathematically that
the eigenvalues of
(10) are real. The mathematical proof follows directly from the
Hermitianness of the energy operator
must be real. Nonetheless, it is as useful exercise and a simple
consistency check on our theory to verify mathematically that
the eigenvalues of
(10) are real. The mathematical proof follows directly from the
Hermitianness of the energy operator 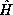 . The proof we give
below is completely general and and may be applied to any Hermitian operator.
. The proof we give
below is completely general and and may be applied to any Hermitian operator.
Prof. Tomas Alberto Arias
Thu Oct 12 16:07:59 EDT 1995
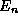 must be real. Nonetheless, it is as useful exercise and a simple
consistency check on our theory to verify mathematically that
the eigenvalues of
(10) are real. The mathematical proof follows directly from the
Hermitianness of the energy operator
must be real. Nonetheless, it is as useful exercise and a simple
consistency check on our theory to verify mathematically that
the eigenvalues of
(10) are real. The mathematical proof follows directly from the
Hermitianness of the energy operator 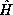 . The proof we give
below is completely general and and may be applied to any Hermitian operator.
. The proof we give
below is completely general and and may be applied to any Hermitian operator.