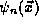 is that
they are orthogonal, the inner product between the pure
states associated with two different energies is always zero,
is that
they are orthogonal, the inner product between the pure
states associated with two different energies is always zero,
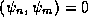 . Again the proof we give is completely
general and is valid for any Hermitian operator.
. Again the proof we give is completely
general and is valid for any Hermitian operator.
A useful property of the energy eigenstates 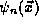 is that
they are orthogonal, the inner product between the pure
states associated with two different energies is always zero,
is that
they are orthogonal, the inner product between the pure
states associated with two different energies is always zero,
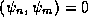 . Again the proof we give is completely
general and is valid for any Hermitian operator.
. Again the proof we give is completely
general and is valid for any Hermitian operator.

If we agree to normalize our eigenstates properly so that 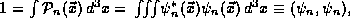 we then may write compactly
we then may write compactly

where 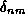 is the Kronecker
is the Kronecker 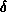 -function, which is
defined as
-function, which is
defined as
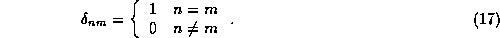
With this understood, the determination of the constants 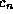 in the
general expansion
in the
general expansion
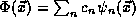 is now simple. To extract
is now simple. To extract 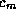 ,
we just take the inner product of
,
we just take the inner product of 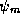 with
with 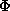 ,
,

With the 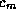 we now may compute
the probabilities of measuring the value
we now may compute
the probabilities of measuring the value 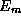 in an experiment,
in an experiment,
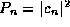 . We may also use them to give an explicit form for the
expansion of an arbitrary state
. We may also use them to give an explicit form for the
expansion of an arbitrary state 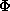 in terms of the pure energy
states
in terms of the pure energy
states 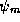 ,
,