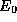We now move to more physical statements about the behavior of the solutions of the TISE. The first of these is the variational principle.
In its simplest form, the variational principle is the mathematical
expression of the physically sensible
statement that the average energy observed for a system in any
quantum state must be at least as large as the lowest energy state
(ground state) of the system,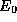 
. Despite its apparent
simplicity, this principle is extremely powerful and forms the basis
for the vast majority of large scale quantum calculations carried
out in current research.
To express this principle mathematically, we begin with an
arbitrary, not necessarily normalized wavefunction, 
. To
compute the average energy of the state described by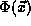 
we
must first normalize
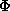by dividing by the square root of the
inner product of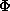 
with itself,
.
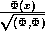This function is now properly normalized
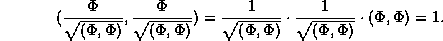
From the properly normalized state, we may compute the average energy,
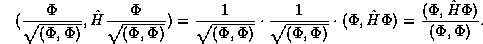
The quotient
has a special name and is known as the Rayleigh quotient.
The variational principle states that the Rayleigh
quotient is never be less than the ground state energy.
Because the Rayleigh quotient takes on the value of the
ground state energy when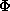 
is the ground state,
the mathematical expression of the variational principle is the
statement that the function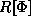 
has its
minimum at the ground state energy,
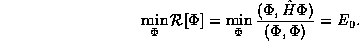
We shall prove an even more general version of this statement. The
minimum of a function is just a special case of a critical or
stationary point. A stationary point, like the minimum, is an input
value in
the domain of a function where all of the first derivatives of
a function are zero. This means that if we move slightly away from a
critical point, the value of the function changes only slightly and varies
only to second order in the distance from the critical
point. We refer to the nearly constant behavior of a function near
a critical point by saying that the function is
stationary about the critical points. We will now show that the
variational principle:
Variational Principle: the Rayleigh quotient 
is
stationary about all of the eigenstates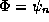 
.
Phrased in this more general way, the variation principle may be used
to help identify excited as well as ground states. We will see
an example of how this principle may be used in the next section where
we use it to prove an extremely general version of the virial theorem.
To prove the stationary property of the Rayleigh quotient, imagine
that we are in the vicinity of one of the
eigenstates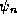 
so that 
, where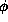 
is
relatively small. Using (20) we may decompose
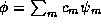, where because 
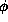is small, the 
will be
small also. To prove that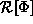 
is stationary about 
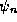we
now just have to show that the Rayleigh
quotient is nearly constant,
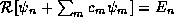to first order in the 
.
We proceed by first expanding the denominator and then the numerator of
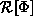, both to second order in the 
. The expansion of the
denominator is
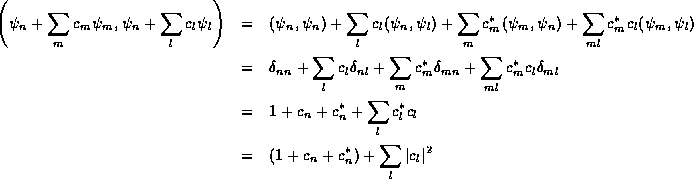
The expansion of the numerator is quite similar,
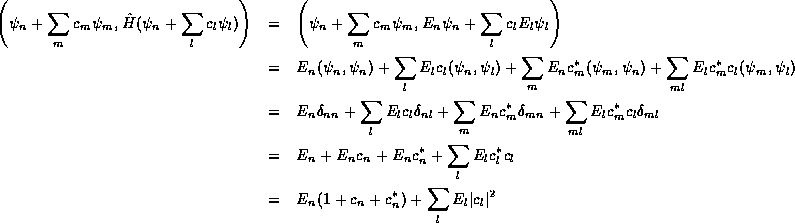
Finally, we combine our two results
Here we have kept our expression correct up to and including second
order terms in the c's, lumping all third and higher order
terms together in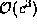 
. We see that there are no correction
terms first order in the c's. 
is therefore stationary
about the value 
, which is what we had wanted to prove.
Moreover, we immediately see that 
if n=0 is the
ground state, and thus the corrections are always positive near the
ground state. Thus we also see that 
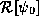is a minimum about
the ground state as promised.