Aside from its value in computer calculations, the variational principle is a very powerful theoretical tool. It allows us to prove an extremely general result, the Virial theorem, regarding the averages of the various terms in the energies for systems in pure energy states. In its most general form, the Virial theorem is true even for systems containing of many particles such as macroscopic objects.
The virial theorem states that if the potential energy function
of a
system of N particles is a homogeneous function of order v of the
coordinates,
then for each and every pure state n of the total energy operator 
of energy 
the average kinetic energy 
and average
potential energy 
of the system must obey
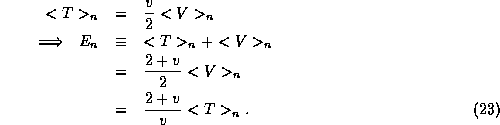
Examples we have see so far of this are the simple harmonic oscillator
, the Hydrogen atom
, and the bouncing ball 
. We have also touched on a multiple particle system which fits
into this framework as well, the multiple electron atom. In fact, any
system composed of electrons and nuclei, such as yourself,
satisfies the conditions of the virial theorem. By far the
most important force in systems composed of electrons and nuclei is
the electrostatic force. In the case of a single
atom, if 
is the position of the nucleus of charge Z and
are the positions of the Z electrons,
then we have N=Z+1 particles and 
In this case and
cases with more than one nuclei, V is still a homogeneous
function of order v=-1.
In all of these cases, the virial theorem allows us to make exact quantum mechanical statements about the pure energy states of systems,
