


Next: Proof
Up: Virial Theorem
Previous: Virial Theorem
The formal part of this course deals almost
exclusively with systems of one particle. While we have not yet
discussed all the the physics of multiple particle systems, the
general considerations we have laid out so far are sufficient for us to
formulate and give a valid proof the virial theorem in the general
case of more than one particle.
Within our framework, a systems of N particles is described by the
coordinates of the particles in the system 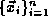 .
Measurements of the positions of the particles in the system will
lead to a distribution of results, where some probability
function
.
Measurements of the positions of the particles in the system will
lead to a distribution of results, where some probability
function  describes the probability of finding a
particle in the small volume
describes the probability of finding a
particle in the small volume 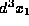 around
around 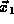 and another
particle in the volume
and another
particle in the volume 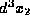 about
about 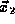 and so forth for all
of N particles in the system. For a given quantum state
and so forth for all
of N particles in the system. For a given quantum state  of
the system, this probability is given by the square of a quantum
probability amplitude
of
the system, this probability is given by the square of a quantum
probability amplitude 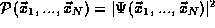 .
The wavefunction of the
.
The wavefunction of the 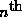 pure state of energy will be an
eigenstate of the Hamiltonian (total energy) operator,
pure state of energy will be an
eigenstate of the Hamiltonian (total energy) operator,
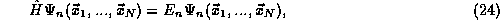
where the Hamiltonian 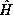 is the sum of the total kinetic and
potential energy operators,
is the sum of the total kinetic and
potential energy operators,
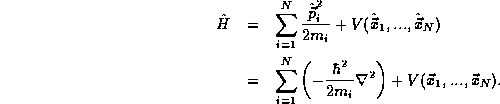
There is only one other fact about multiple particle systems, the
Pauli Exclusion Principle, which puts additional constraints on the
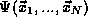 beyond those imposed by the Time Independent
Schrödinger Equation (25). We will discuss this
principle in a later note. All that we will need for now to
demonstrate the virial theorem is the knowledge that
beyond those imposed by the Time Independent
Schrödinger Equation (25). We will discuss this
principle in a later note. All that we will need for now to
demonstrate the virial theorem is the knowledge that 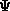 satisfies condition (25).
satisfies condition (25).
Prof. Tomas Alberto Arias
Thu Oct 12 16:07:59 EDT 1995
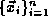 .
Measurements of the positions of the particles in the system will
lead to a distribution of results, where some probability
function
.
Measurements of the positions of the particles in the system will
lead to a distribution of results, where some probability
function  describes the probability of finding a
particle in the small volume
describes the probability of finding a
particle in the small volume 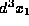 around
around 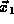 and another
particle in the volume
and another
particle in the volume 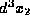 about
about 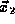 and so forth for all
of N particles in the system. For a given quantum state
and so forth for all
of N particles in the system. For a given quantum state  of
the system, this probability is given by the square of a quantum
probability amplitude
of
the system, this probability is given by the square of a quantum
probability amplitude 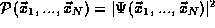 .
The wavefunction of the
.
The wavefunction of the 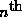 pure state of energy will be an
eigenstate of the Hamiltonian (total energy) operator,
pure state of energy will be an
eigenstate of the Hamiltonian (total energy) operator,
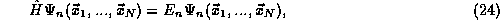
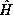 is the sum of the total kinetic and
potential energy operators,
is the sum of the total kinetic and
potential energy operators,
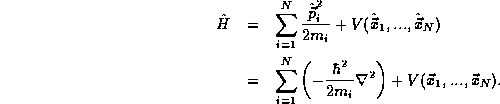
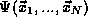 beyond those imposed by the Time Independent
Schrödinger Equation (
beyond those imposed by the Time Independent
Schrödinger Equation (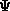 satisfies condition (
satisfies condition (