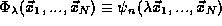 then
then 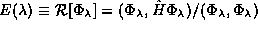 is stationary
about the value
is stationary
about the value 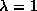 (
(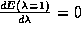 )
because here
)
because here 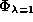 is just the
eigenstate
is just the
eigenstate  . To prove the virial theorem
we now evaluate
. To prove the virial theorem
we now evaluate 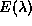 and set
and set 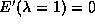 .
.
With the variational principle and the multiple particle Schrödinger
equation in hand, the mathematics of the proof of the virial theorem
is straight forward. Our proof will be based on the observation from
the variational principle that if we ``dilate'' one of the eigenstates
taking 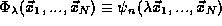 then
then 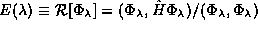 is stationary
about the value
is stationary
about the value 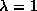 (
(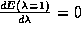 )
because here
)
because here 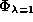 is just the
eigenstate
is just the
eigenstate  . To prove the virial theorem
we now evaluate
. To prove the virial theorem
we now evaluate 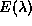 and set
and set 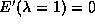 .
.
First, we evaluate the denominator of 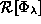 ,
,
Next we break the numerator into potential and kinetic parts,
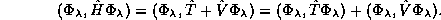
The potential part gives,
We now finish with the kinetic energy part which is a bit more difficult because of the differential form of the kinetic energy operator.
Putting (26-28) together we have,

As discussed above, this 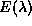 must be stationary about
must be stationary about
 ,
,
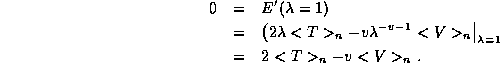
From this follows directly the general virial theorem
for systems with homogeneous potential interactions  ,
,
