We now complete our general discussion of scattering theory by verifying explicitly that the formulae (15), which were derived from different beam components of a single stationary solution to the TISE do indeed give the correct normalizations of the reflected and transmitted parts of an incoming wave packet.
The total probability associated with each of the packets is best determined in momentum space. From 17 is it clear that the momentum space wave function representation of the source packet at time t is
![]()
so that the total probability associated with the source packet is
![]()
We know that the total probability associated with ![]() must be
one because for t;SPMlt;;SPMlt;0, this is the only one of the packets which
makes a contribution to the time dependent wave function, which always
much be normalized.
must be
one because for t;SPMlt;;SPMlt;0, this is the only one of the packets which
makes a contribution to the time dependent wave function, which always
much be normalized.
To determine the momentum space representation of ![]() , for
the purpose of finding the probability of reflection
, for
the purpose of finding the probability of reflection ![]() , we
must manipulate (18) into the form of a standard
Fourier transform. We may accomplish this by making the change of
variables
, we
must manipulate (18) into the form of a standard
Fourier transform. We may accomplish this by making the change of
variables ![]() . Under such a change of variables,
. Under such a change of variables,
![]() , so that k is simply
replaced by -k in the integrand I(k). Applying this to
(18) then gives us
, so that k is simply
replaced by -k in the integrand I(k). Applying this to
(18) then gives us
where in the last step we have changed back to the original k
variable by making the change ![]() once again. This is
the complete, exact expression for the reflection probability.
Generally, we deal in the narrow packet approximation under
which
once again. This is
the complete, exact expression for the reflection probability.
Generally, we deal in the narrow packet approximation under
which ![]() , much like a Dirac
, much like a Dirac ![]() function is so
concentrated about
function is so
concentrated about ![]() that neither r(k) nor t(k) vary
significantly over the range of k for which
that neither r(k) nor t(k) vary
significantly over the range of k for which ![]() is
appreciable. Under these circumstances, |r(k)| may be replaced to a
good approximation by its value at
is
appreciable. Under these circumstances, |r(k)| may be replaced to a
good approximation by its value at ![]() , so that
, so that
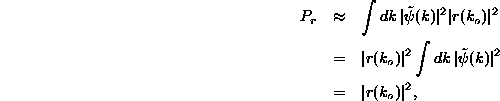
which is what we found in (15) based on the probability current.
To determine the full, exact form of the probability of
transmission ![]() , we require the momentum space representation of
, we require the momentum space representation of
![]() . To do this we
note that (19) does not appear in the standard
momentum representation form because the variable of integration, k,
is not the same wave vector which appears describing the pure momentum
states,
. To do this we
note that (19) does not appear in the standard
momentum representation form because the variable of integration, k,
is not the same wave vector which appears describing the pure momentum
states, ![]() . To produce the more familiar form, we should thus
change the variable of integration to
. To produce the more familiar form, we should thus
change the variable of integration to ![]() . (12)
gives the relationship between
k and
. (12)
gives the relationship between
k and ![]() so that we may perform the change of variables in
(19).
so that we may perform the change of variables in
(19).
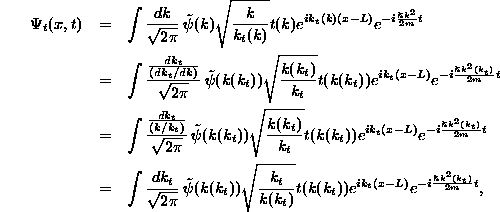
where we have used ![]() from (23) and have
taken care to write everything now as a function of k. If needed,
the function
from (23) and have
taken care to write everything now as a function of k. If needed,
the function ![]() is easily determined by inverting (12).
Now that we have the standard form of the momentum superposition, we may
pick-off the momentum space wave function, now in terms of
is easily determined by inverting (12).
Now that we have the standard form of the momentum superposition, we may
pick-off the momentum space wave function, now in terms of ![]() instead of k, thereby using in effect Parseval's theorem to determine the
normalization of transmitted packet,
instead of k, thereby using in effect Parseval's theorem to determine the
normalization of transmitted packet,
Here again, we have used the identity (23), and in our
last step changed the integration variable back to k. This is the
full, exact expression for ![]() . As with the reflected packet,
it is easy to determine the transmission probability when working in the
narrow packet limit,
. As with the reflected packet,
it is easy to determine the transmission probability when working in the
narrow packet limit,

which is what we found in (15) based on the probability current.
There are two important lessons to be learned from this section.
First, the results (15) determined using the simpler
idea of monitoring the transmitted and reflected contributions to the
current were indeed correct, but only when the packet is very narrowly
distributed in momentum space. It is important to keep this caveat in
mind. In some cases in scattering theory, particularly in the study
of resonance, r(k) and t(k) become very sharply peaked, so that it
becomes very demanding to produce incoming wave packets with
![]() which is truly narrowly peaked in comparison. The second
lesson is that there are more exact expressions available
(24,25) for the reflection and
transmission probabilities in cases where the packet is not so narrow.
which is truly narrowly peaked in comparison. The second
lesson is that there are more exact expressions available
(24,25) for the reflection and
transmission probabilities in cases where the packet is not so narrow.