


Next: Traveling waves making up
Up: ps6
Previous: Problem 3
Contents
- (a)
- Show that the expression
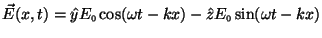 |
(1) |
is a solution to the wave equation for
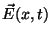 .
.
- (b)
- In our discussion of simple harmonic motion we
introduced the complex representation by writing the
solution to the Equation of Motion as
![$ \Re\mathfrak{e}\left[\underline{A}
e^{i\omega t}\right]$](img13.png) , with
, with
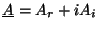 . Using a similar
technique, show that the solution (1) can be written
in the form
. Using a similar
technique, show that the solution (1) can be written
in the form
![$\displaystyle \vec{E}(x,t) = \Re\mathfrak{e}\left[\left(\hat{y}+i\hat{z}\right) E_{\scriptscriptstyle 0}e^{i(\omega t - kx)}\right]\;,$](img15.png) |
(2) |
where
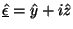 is the
complex polarization vector. Such a wave is called
``circularly polarized''.
is the
complex polarization vector. Such a wave is called
``circularly polarized''.
- (c)
- The (equivalent) expressions (1) and
(2) represent the
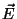 -field of an EM wave
travelling along the
-field of an EM wave
travelling along the  -axis. Derive an equation for the magnetic
field of this wave,
-axis. Derive an equation for the magnetic
field of this wave,
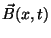 both in real and in complex
representation.
both in real and in complex
representation.
- (d)
- Draw two snapshots of the waveform, at times
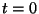 and
and
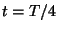 , i.e., for each of these times draw
, i.e., for each of these times draw
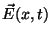 and
and
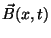 (both magnitudes and directions) for at least 5
equally spaced positions in the interval
(both magnitudes and directions) for at least 5
equally spaced positions in the interval
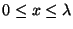 .
Can you now tell why this type of E & M wave is called
``circularly polarized''?
.
Can you now tell why this type of E & M wave is called
``circularly polarized''?



Next: Traveling waves making up
Up: ps6
Previous: Problem 3
Contents
Tomas Arias
2003-10-08