


Next: About this document ...
Up: ps6
Previous: Traveling waves making up
Contents
(Be sure to ask in section if you have
difficulties with this problem!)
In this question, ignore reflections from the ends of the
strings (assume the ends are at
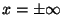 ).
).
- (a)
- At t = 0, a string is plucked. This means the string is
initially motionless
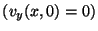 and has a given initial
shape--shown on Figure 1. Consider the form of the general
solution of the wave equation
and has a given initial
shape--shown on Figure 1. Consider the form of the general
solution of the wave equation
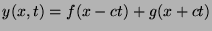 .
What must the relationship between
.
What must the relationship between 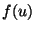 and
and 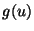 be, given that
the string is initially motionless?
be, given that
the string is initially motionless?
Figure 1:
Plucked string.
|
|
- (b)
- Sketch what the string looks like at
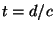 and
and 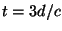 .
.
- (c)
- At
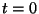 , the hammer of a piano hits a piano string
centered at point
, the hammer of a piano hits a piano string
centered at point 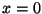 . In a simplified model, the string is
perfectly flat at
. In a simplified model, the string is
perfectly flat at 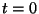 , but the hammer has given it an initial
velocity distribution
, but the hammer has given it an initial
velocity distribution 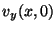 . Consider the form of the
general solution of the wave equation
. Consider the form of the
general solution of the wave equation
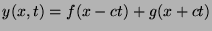 . What must the relationship between
. What must the relationship between 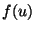 and
and 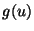 be
given that the string is initially flat?
be
given that the string is initially flat?
- (d)
- The function
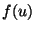 for the piano string is sketched on
Figure 2. Use it to sketch the initial velocity
distribution
for the piano string is sketched on
Figure 2. Use it to sketch the initial velocity
distribution 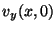 .
.
Figure 2:
The function 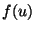 for a piano string.
for a piano string.
|
|
- (e)
- Sketch what the piano string looks like at
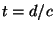 and
at
and
at 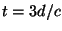 .
.



Next: About this document ...
Up: ps6
Previous: Traveling waves making up
Contents
Tomas Arias
2003-10-08
![]() ).
).