


Next: Using Interference to Study
Up: ps8
Previous: The Two Towers
Contents
Phasors provide a convenient way to analyze interference phenomena.
A phasor is simply a two-dimensional vector that represents a complex
number: the 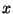 -component of a phasor represents the real (
-component of a phasor represents the real (
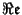 )
part of a complex number and the
)
part of a complex number and the 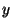 -component represents the imaginary
(
-component represents the imaginary
(
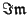 ) part. The polar representation of complex numbers
also has a neat geometric interpretation with phasors: the angle that
the phasor makes with the
) part. The polar representation of complex numbers
also has a neat geometric interpretation with phasors: the angle that
the phasor makes with the 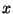 -axis represents the phase of the complex
number, and the length of the phasor represents its magnitude. To
represent a sum of two or more complex numbers, you can now simply
add the corresponding phasors, using the usual rules of vector addition.
-axis represents the phase of the complex
number, and the length of the phasor represents its magnitude. To
represent a sum of two or more complex numbers, you can now simply
add the corresponding phasors, using the usual rules of vector addition.
Example: the sum
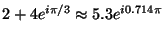 can be represented by the phasor diagram in Fig. 4.
can be represented by the phasor diagram in Fig. 4.
Figure 4:
Adding complex numbers with phasors.
|
|
We can use phasors to illustrate the sum inside the absolute value
bars in Eq. (8) (p. 7 of the Class Notes ``Wave Phenomena II:
Interference''.) Each phasor represents the
complex amplitude of the light coming from one source. When we sum
these phasors, the resultant phasor represents the complex amplitude
of the superposition of light coming from all of the sources.
Example: A minimum for three equivalent narrow slits can result
from either of the phasor sums in Fig. 5.
Figure:
Phasor diagram for 3-slit interference.
|
|
Draw the phasor diagrams to illustrate the following cases of interference.
Label magnitudes and angles. If there is more than one possibility (as in
the example above), illustrate all of them.
- (a)
- Principal maximum for 5 narrow slits;
- (b)
- Minimum for 5 narrow slits ;
- (c)
- Secondary maximum for 4 narrow slits (don't worry
about making the angles exact--an approximation is fine);
- (d)
- Minimum for 2 narrow slits where one is three times as wide
as the other (
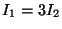 ).
).



Next: Using Interference to Study
Up: ps8
Previous: The Two Towers
Contents
Tomas Arias
2003-10-22
![]() can be represented by the phasor diagram in Fig. 4.
can be represented by the phasor diagram in Fig. 4.