Example of sum over histories

As a more involved example of the sum over histories, consider transmission of waves of wave vector $k_a$ on a string $a$ of tension and mass per unit length $\tau$ and $\mu_a$ through a barrier made up of a short segment of a heavier string of mass per unit length $\mu_b > \mu_a$ and length $b$. (See Figure 2.) Note that because the segments of the string are in equilibrium before we allow any wave motion, the horizontal tensions $\tau$ in all segments must be equal.

Figure 2: Transmission of waves through a barrier on a string

The relevant quantities for propagation in this problem are the respective wave speeds, $c_a=\sqrt{\tau/\mu_a}$ and $c_b=\sqrt{\tau/\mu_b}$, and the impedances,

$$Z_a \equiv \mu_a c_a = \sqrt{\tau \mu_a}$$ (16)

$$Z_b \equiv \mu_b c_b = \sqrt{\tau \mu_b}.$$

We also require the wave vector in the heavy region, which we determine from the fact that the response of the system in all regions will be at the same frequency as the incoming wave. Thus, $c_a k_a = \omega = c_b k_b$, so that

$$k_b= \frac{c_a}{c_b} k_a = \left(\sqrt{\frac{\mu_b}{\mu_a}}\right) k_a.$$ (17)

Finally, we will need the following scattering amplitudes,

$$R_{b \rightarrow a} = \frac{Z_b-Z_a}{Z_a+Z_b}$$ (18)

$$T_{a \rightarrow b} = \frac{2 Z_a}{Z_a+Z_b}$$

$$T_{b \rightarrow a} = \frac{2 Z_b}{Z_a+Z_b}$$

With the above quantities defined, we can now compute the transmission amplitude for passing through the barrier. Following (12), we must consider all possible histories contributing to transmission through the barrier. The first three of these appear in the figure. In the first history, $h_1$, the wave transmits from string $a$ to $b$, picking up a transmission amplitude factor $T_{a \rightarrow b}$, propagates across from $x=0$ to $x=b$, picking up a phase factor $p\equiv e^{ik_b b}$, and finally transmits from string $b$ to string $a$, picking up a final transmission amplitude factor $T_{b \rightarrow a}$. The first contribution to the transmitted wave is thus $T_{a \rightarrow b} p T_{b \rightarrow a}$.

The next contribution, $h_2$, comes from when the wave transmits from $a$ to $b$, propagates across, but then reflects at the interface from $b$ to $a$ at $x=b$, picking up a new factor of $R_{b \rightarrow a}$. This wave then propagates back across from $x=b$ to $x=0$, picking up the same phase factor $p\equiv e^{ik_b b}$ as before because the distance propagated is the same. At $x=0$, the wave then reflects again with a factor $R_{b \rightarrow a}$, propagates back across the barrier with a factor of $p$, and finally transmits from $b$ into $a$ with a factor of $T_{b \rightarrow a}$. The contribution from this history is the product of all of these factors, $T_{a \rightarrow b} p R_{b \rightarrow a} p R_{b \rightarrow a} p T_{b \rightarrow a}$.

There is then a third contribution, $h_3$, which involves yet another ricochet in between the barriers. After this contribution, there is actually an infinite sequence of terms $h_{n>3}$, each involving one more ricochet than the previous term in the sequence.

Combining all of these terms, we thus write (12) for this case as

$$\begin{eqnarray*} Q(b) & = & Q(0) \sum_h \left( \prod_{e \in h} a_e \right) \\ ... ...a}}{1-\left(p R_{b \rightarrow a} p R_{b \rightarrow a}\right)}, \end{eqnarray*}$$

where in the last step we use the calculus result for the sum of an infinite geometric series $1+\underline{r}+\underline{r}^2 + \ldots = 1/(1-\underline{r})$. Note that in the analysis above, we could at any step have simplified $p R_{b \rightarrow a} p R_{b \rightarrow a} = p^2 R_{b \rightarrow a}^2$. We have chosen not to do so only as a way of reminding ourselves of the sequence of events underlying each term in the series.

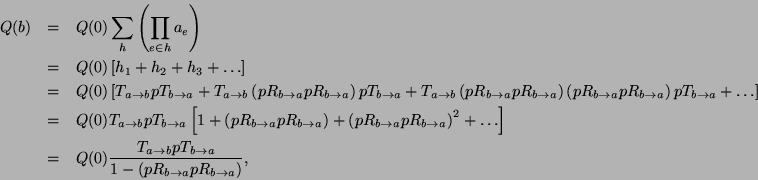
Finally, the net transmission amplitude for the barrier, $T_{\mathrm{barrier}} \equiv Q(b)/Q(0)$, is thus

$$T_{\mathrm{barrier}} = \frac{T_{a \rightarrow b} p T_{b \rightarrow a}}{1-p^2 R_{b \rightarrow a}^2},$$ (19)

where $p\equiv e^{ik_b b}$ and all other relevant quantities are defined in (16-18).