


Next: Example of sum over
Up: Complex Represenation of Waves
Previous: General Lesson
Contents
Now that we are able to write down the forms (8) and
(10) directly,
it is then a relatively simple matter to compute scattering amplitudes
such as
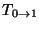 and
and
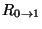 directly from the boundary conditions.
For notational convenience, in this section we shall drop
the writing of the subscripts ``
directly from the boundary conditions.
For notational convenience, in this section we shall drop
the writing of the subscripts ``
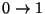 '' and refer to these
amplitudes as
'' and refer to these
amplitudes as 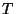 and
and 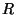 , respectively.
Eqs. (8,10) then become
, respectively.
Eqs. (8,10) then become
Substituting (13) into the consistency condition,
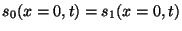 , we find
, we find
so that
Now,
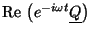 can only be zero for all
times
can only be zero for all
times 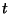 if the harmonic motion which it represents has zero
amplitude, which implies
if the harmonic motion which it represents has zero
amplitude, which implies
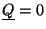 . We thus conclude
. We thus conclude
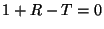 , so that
, so that
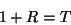 |
(14) |
Next, substituting (13) into the force balance
condition,
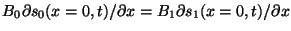 , we find
, we find
where the factors of 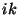 come down as we take the derivatives with
respect to
come down as we take the derivatives with
respect to 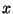 before substituting
before substituting 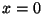 . Combining terms we find
. Combining terms we find
for all times 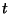 . Following the same logic which led to
(14), we find
. Following the same logic which led to
(14), we find
Using the fact that
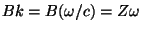 , this
simplifies to
, this
simplifies to
Finally, to find the reflection and transmission amplitudes, we
combine (14) and (15). To find 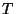 , we
take
, we
take 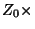 (14)
(14)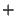 (15):
(15):
This gives precisely our previous result,
And, to find 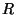 , we take
, we take 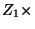 (14)
(14) (15):
(15):
Again, we find our previous result,

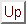


Next: Example of sum over
Up: Complex Represenation of Waves
Previous: General Lesson
Contents
Tomas Arias
2003-10-27
![]() and
and
![]() directly from the boundary conditions.
For notational convenience, in this section we shall drop
the writing of the subscripts ``
directly from the boundary conditions.
For notational convenience, in this section we shall drop
the writing of the subscripts ``
![]() '' and refer to these
amplitudes as
'' and refer to these
amplitudes as ![]() and
and ![]() , respectively.
Eqs. (8,10) then become
, respectively.
Eqs. (8,10) then become
![]() , we find
, we find
![\begin{eqnarray*}
{\mbox{Re\,}}\left(e^{-iwt} \underline{A} \left[ e^{ik_0 \cdot...
...box{Re\,}}\left(e^{-iwt} \underline{A} \left[ T \right] \right),
\end{eqnarray*}](img98.png)
![]() , we find
, we find
![\begin{eqnarray*}
B_0 {\mbox{Re\,}}\left(e^{-iwt} \underline{A} \left[ ik_0 e^{i...
...\left(e^{-iwt} \underline{A} B_1 \left[
ik_1 T \right] \right),
\end{eqnarray*}](img105.png)
![]() , we
take
, we
take ![]() (14)
(14)![]() (15):
(15):