


Next: General Lesson
Up: Solutions for waves at
Previous: Region 0
Contents
Eq. (5) also gives the solution in Region 1,
where, in the second line from the bottom, we have used the dispersion
relation of Region 1 to identify
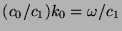 as just the
wave vector
as just the
wave vector 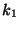 from Region 1. Also, in the last line we define a
new complex amplitude for the wave motion in Region 1,
from Region 1. Also, in the last line we define a
new complex amplitude for the wave motion in Region 1,
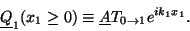 |
(11) |
Thus, we once again find that all points in the system respond with
simple harmonic motion at the same driving frequency 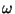 , so that
knowledge of
, so that
knowledge of
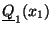 completely determines the motion in
Region 1. For instance, the amplitude of the motion for each point in
Region 1 is
completely determines the motion in
Region 1. For instance, the amplitude of the motion for each point in
Region 1 is
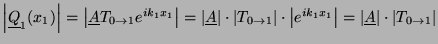 , just the amplitude of the
incoming wave times the magnitude of the transmission amplitude.
, just the amplitude of the
incoming wave times the magnitude of the transmission amplitude.
Finally, we see that we can again write this result directly in terms
of relative complex amplitudes. Relative to the motion at point
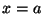 , the motion of the transmitted wave at
, the motion of the transmitted wave at 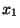 should contain
a factor of
should contain
a factor of 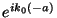 to give the motion of the incoming wave at
to give the motion of the incoming wave at
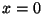 , a factor of
, a factor of
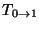 to give the motion of the
transmitted wave at
to give the motion of the
transmitted wave at 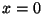 relative to the motion of the incoming wave
at the same point, and a factor of
relative to the motion of the incoming wave
at the same point, and a factor of 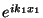 to give the motion of
the traveling wave after propagating the distance
to give the motion of
the traveling wave after propagating the distance 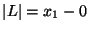 from
from
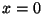 to the point
to the point 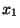 . We thus can immediately write a result
equivalent to (10),
. We thus can immediately write a result
equivalent to (10),
Note that in the case we do not have a sum of terms because only a
single wave contributes to the motion in Region 1. (See
Figure 1.)



Next: General Lesson
Up: Solutions for waves at
Previous: Region 0
Contents
Tomas Arias
2003-10-27
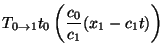
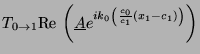
![]() , the motion of the transmitted wave at
, the motion of the transmitted wave at ![]() should contain
a factor of
should contain
a factor of ![]() to give the motion of the incoming wave at
to give the motion of the incoming wave at
![]() , a factor of
, a factor of
![]() to give the motion of the
transmitted wave at
to give the motion of the
transmitted wave at ![]() relative to the motion of the incoming wave
at the same point, and a factor of
relative to the motion of the incoming wave
at the same point, and a factor of ![]() to give the motion of
the traveling wave after propagating the distance
to give the motion of
the traveling wave after propagating the distance ![]() from
from
![]() to the point
to the point ![]() . We thus can immediately write a result
equivalent to (10),
. We thus can immediately write a result
equivalent to (10),