Solutions for waves at an interface

The previous set of notes ``Reflection and Transmission at a Change in Medium,'' gives the general solution for waves at a change in medium from Region 0 (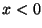$x<0$) to Region 1 (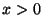$x>0$) as

$$s_0(x \le 0,t) = t_0(x-c_0 t) + R_{0 \rightarrow 1} t_0\left(-(x+c_0 t)\right) + T_{1 \rightarrow 0} t_1\left(\frac{c_1}{c_0} (x+c_0 t) \right)$$ (5)

$$s_1(x \ge 0,t) = t_1(x+c_1 t) + R_{1 \rightarrow 0} t_1\left(-(x-c_1 t)\right) + T_{0 \rightarrow 1} t_0\left(\frac{c_0}{c_1} (x-c_1 t)\right).$$

Our strategy is to begin with this form, investigate what it looks like in the complex representation, and then see how we could immediately write down the result in the complex representation.

Sending a sinusoidal pulse in from Region 0 (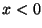$x<0$) toward Region 1 corresponds to the case

$$t_0(u) = {\mbox{Re\,}}\left(\underline{A} e^{ik_0u}\right)$$ (6)

$$t_1(v) = 0,$$ (7)

where we use the subscript on 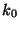$k_0$ to be sure to label it as the wave vector in Region 0.